NOVEMBER 2018 PUZZLE - "A Stimulus / Response Enigma"

Submitted by Dave Thomas

A common device with a digital keypad for data entry has a certain response for an input of 170, and twice that response for an input of 420. The first response is also the result of inputting 210, and the response is likewise doubled when 380 is used as input.

The November Bonus: What is the device? And what are the two actual responses?

Hall of Fame (November Puzzle Solvers):

Earl Dombroski (NM)
Allen Robnett (NM)
Harold H. Gaines (KS)
Rocky S. Stone (NM)

OCTOBER 2018 PUZZLE - "What Comes Next?"

Submitted by Dave Thomas

Here are some values in a sequence. They appear one after the other, starting with the one on the left.

The October Bonus: What comes next?

Hall of Fame (October Puzzle Solvers):

Rocky S. Stone (NM)
Mike Arms (NM)
Earl Dombroski (NM)
Allen Robnett (NM)
Harold H. Gaines (KS)
Austin Moede (NM)
Terry Lauritsen (NM)

SEPTEMBER 2018 PUZZLE - "Uphill is Downhill (On the Return Trip)"

Submitted by Dave Thomas

A bicycling commuter can go 6 mph uphill, 8 mph on level road, and 12 mph downhill. It takes him 17 and a half minutes to get to work in the morning, and 12 and a half minutes to return home in the afternoon.

The September Bonus: (A) How far is it to work? (B) On the way to work, how many more miles are spent going uphill than are spent going downhill? (C) What are the minimum and maximum values of level riding possible?

Hall of Fame (September Puzzle Solvers):

Earl Dombroski (NM)
Paul Braterman (UK)
Mike Arms (NM)
Allen Robnett (NM)
Gene Aronson (NM)

AUGUST 2018 PUZZLE - "Lord of the Rings"

Submitted by Dave Thomas

Samwise wants to make a friendship bracelet for Frodo, but all he has are five separate pieces of gold chain, as shown here.

Gandalf has offered to cast a spell allowing one ring to be opened, and then closed, after an interval of just ten seconds. However, the wizard insists on the condition that Samwise asks him to use that spell the absolute minimum number of times.

The August Bonus: How many spells must Gandalf invoke to complete the bracelet? (i.e., how many rings must he work on?)

Hall of Fame (August Puzzle Solvers):

Earl Dombroski (NM)
Allen Robnett (NM)
George Egert (NM)
Keith Gilbert (NM)
Austin Moede (NM)
Rocky S. Stone (NM)
Terry Lauritsen (NM)
Mike Arms (NM)

JULY 2018 PUZZLE - "Powered Ascent"

Submitted by Dave Thomas

A bored convention-goer decided to deduce how many steps were found from the bottom to the top of the up escalator in the lobby. She found that by simply standing on the same step, she would ascend to the top in 35 seconds. When she walked up the moving escalator at her normal pace, however, the ascent only took 15 seconds, with a total of 23 steps climbed.

The July Bonus: If the power was switched off, and the escalator became mere stairs, how many steps is it to the top? And how long would it take our subject to make the ascent?

Hall of Fame (July Puzzle Solvers):

Earl Dombroski (NM)
Paul Braterman (UK)
Allen Robnett (NM)
Gene Aronson (NM)
Mike Arms (NM)
Dan Tandberg (NM)

JUNE 2018 PUZZLE - "Emoji Maths"

Submitted by Dave Thomas

The June Bonus: Solve for , given:

Hall of Fame (June Puzzle Solvers):

Earl Dombroski (NM)
Rocky S. Stone (NM)
Mike Arms (NM)
Keith Gilbert (NM)
Gene Aronson (NM)
Mark Maravetz (NM)
Allen Robnett (NM)
Eiichi Fukushima (NM)

MAY 2018 PUZZLE - "Construction Delay"

Submitted by Dave Thomas

The May Bonus: A commuter normally drives at 80 mph for an hour to reach his destination. He has found that a stretch of new construction on his route, with a strict 50 mph limit, adds nine minutes to his normal commute.

The May Bonus: How long is the construction zone?

Hall of Fame (May Puzzle Solvers):

Eiichi Fukushima (NM)
Keith Gilbert (NM)
Earl Dombroski (NM)
Paul Braterman (UK)
Rocky S. Stone (NM)
Gene Aronson (NM)
Mike Arms (NM)
Terry Lauritsen (NM)

APRIL 2018 PUZZLE - "Run, Fastman, Run"

Submitted by Dave Thomas

The April Bonus: Two trains are approaching each other on adjacent tracks, and each is moving at 60 mph with respect to the ground. The world’s fastest man, Fastman, departs from train #1 when the two trains are 120 miles apart. When he gets to train #2, Fastman turns around instantly, and heads back toward train #1, then turns again and heads back to train #2, and so forth. This continues until the two trains meet, at which time Fastman stops.
Fastman is running faster (constant speed w) than the trains (constant speed v=60mph). How fast? Your big clue is that the length of each leg in Fastman’s back-and-forth run is one quarter the length of the preceding leg.

The April Bonus: How far does Fastman run altogether?

Hall of Fame (April Puzzle Solvers):

Allen Robnett (NM)
Earl Dombroski (NM)
Paul Braterman (UK)
Rocky S. Stone (NM)
Gene Aronson (NM)
Keith Gilbert (NM)

MARCH 2018 PUZZLE - "Chicken Futures"

Submitted by Dave Thomas; Based on a True Story

The March Bonus: At the sprawling Wally World store, the deli prices for about equal numbers of chicken legs, thighs, breasts and wings are:

• 8 pieces $5.98
• 16 pieces $10.98
• 50 pieces $54.00
• 100 pieces $75.00

The March Bonus: You are in charge of getting fried chicken for the big party, and you have a budget of $100. Chicken is tax-free, by the way.
What is the largest number of pieces you can purchase at Wally World?

Hall of Fame (March Puzzle Solvers):

Earl Dombroski (NM)
Rocky S. Stone (NM)
Keith Gilbert (NM)
Mike Arms (NM)
Brian Pasko (NM)
Alice Anderson(NM)
Terry Lauritsen (NM)
Gene Aronson (NM)
George Phillips (NM)

FEBRUARY 2018 PUZZLE - "Honest Advertising"

Submitted by Dave Thomas

The February Bonus: Three boxes are all labeled incorrectly, and you must get the labels right. The labels on the boxes read as follows:

To gain the information you need to move the labels to the correct boxes, you may remove a single item from one of the boxes. You may not look into the boxes, nor pick them up and shake them, etc.

The February Bonus: What is the algorithm for success?

Hall of Fame (February Puzzle Solvers):

Keith Gilbert (NM)
Gene Aronson (NM)
Earl Dombroski (NM)
Rocky S. Stone (NM)
Joseph Archbold (NM)
Mike Arms (NM)
Alice Anderson(NM)
Terry Lauritsen (NM)

JANUARY 2018 PUZZLE - "Inner Balance"

Inspired by David Morin, Harvard

The January Bonus:You have a balance, and need to be able to verify any weight from 1 through 121 grams, to the nearest gram. You have a given number of unique fixed weights (called A, B, C, D, … for convenience). You need to be able to weigh unknowns for two different modes of using your balance: Mode #1, in which only the unknown weight is on one scale, and Mode #2, in which some of the fixed weights can also be on the same scale as the unknown.

The January Bonus: What is the minimum number of weights, and what are their values, for Mode #1? For Mode #2?

Hall of Fame (January Puzzle Solvers):

Earl Dombroski (NM)
Paul Braterman (UK)
Rocky S. Stone (NM)

DECEMBER 2017 PUZZLE - "Tug of War"

Submitted by Dave Thomas

Two strong individuals are playing Tug-of-War with a very long, very strong, and very light-weight rope. The two players are strong enough to keep the rope taut, no matter how long it gets. They are playing the game on the Megaville Salt Flats, which are smooth and free of obstructions for hundreds of miles. The players are holding the rope four feet above the ground.

The December Bonus:Assuming that the Earth's radius is 3960 miles, how far apart should the players be for the rope to just touch the ground?

Hall of Fame (December Puzzle Solvers):

Gene Aronson (NM)
Earl Dombroski (NM)
Rocky S. Stone (NM)
Brian Pasko (NM)
Harold H. Gaines (KS)

NOVEMBER 2017 PUZZLE - "Too Early for Sunset?"

Submitted by Dave Thomas

New Orleans, Louisiana has a latitude of 30 degrees North, and a longitude of 90 degrees West. Imagine that you are in NOLA on the day of the summer solstice (June 21st). At noon, you observe the Sun as being directly south. Two hours later, at 2:00 PM, the Sun has moved 15 degrees per hour towards the West, and thus has an azimuth (here, south-towards-west) of 30 degrees.
In the official “Flat Earth” model, the Sun is 40 miles in diameter, and moves above the flat earth at a height of 3,000 miles. On the summer solstice, observers on the Tropic of Cancer (23.50^oN) will see the sun directly overhead at noon.
Therefore, on the solstice, the Flat Earth Sun will move in a circle 3000 miles above the Tropic of Cancer, and will be directly south of New Orleans, and a bit north of the Yucatan (latitude 23.5^oN, longitude 90^oW) at noon.

The November Bonus:Assuming that the Earth is Flat, like the map above:

• What is the latitude/longitude of the Sun at 2:00 PM on the Summer Solstice?
• What is the Azimuth of the Sun at 2:00 PM, as observed from New Orleans, LA?

Hall of Fame (November Puzzle Solvers):

Rocky S. Stone (NM)
Brian Pasko (NM)

OCTOBER 2017 PUZZLE - "How Far the Horizon?"

Submitted by Dave Thomas

Derive the approximation for the distance d to the horizon for an object at height h above the earth, d ~ √2hR, where R = radius of Earth (~ 3960 miles), and also for the angle of dip of the horizon, d/R*180/π in degrees.

The October Bonus:Assuming Mt. Wahdoo-ainoh is five miles above the surrounding terrain, what is the distance to the horizon from its summit? And the Dip Angle of the horizon?

Hall of Fame (October Puzzle Solvers):

Keith Gilbert (NM)
Harold H. Gaines (KS)
Rocky S. Stone (NM)
Allen Robnett (NM)
Gene Aronson (NM)
Brian Pasko (NM)

SEPTEMBER 2017 PUZZLE - "How High the Sun?"

Submitted by Dave Thomas

The diagram below indicates a method whereby one could use measurements of the sun's elevation on the vernal or autumnal equinox to calculate the height of the sun above the earth in Voliva's flat earth model. In this diagram, an observer at 45^o latitude would see the sun at that same angle above the horizon, and will be 1/8th of the 24,000-mile diameter of the flat earth away from the equator, i.e. 3,000 miles. The "height" of the sun would be calculated as 3,000 miles for this latitude.

The September Bonus:What would the following people, using the method above, calculate for the height of the sun above the flat earth, as seen on the autumnal equinox?

• A resident of Albuquerque, NM (latitude 35^o)
• A resident of Eureka, Nunavut, Canada (latitude 80^o)

Hall of Fame (September Puzzle Solvers):

Paul Braterman (UK)
Harold H. Gaines (KS)
Brian Pasko (NM)
Gene Aronson (NM)

AUGUST 2017 PUZZLE - "Uphill Both Ways"

Submitted by Dave Thomas

A commuter using a bicycle has a two-mile ride to work. Going to the office, the path is level for a half mile, then runs uphill at a 10% grade for one mile, then downhill at a 10% grade for a quarter mile, and finally uphill for a quarter mile at a 20% grade. The commuter goes ten mph on a level surface, half that for a 10% uphill grade, three-halves that for a 10% downhill grade, and one-quarter that for a 20% uphill grade. For a 20% downhill grade, the rider purposely limits his speed to no more than that for the 10% downhill grade.

The August Bonus:

• How much higher is the rider’s office above their home, in miles?
• How long does it take the rider to get to work from home?
• How long does it take the rider to get home from work?

Hall of Fame (August Puzzle Solvers):

Mike Arms (NM)
Terry Lauritsen (NM)
Keith Gilbert (NM)
Rocky S. Stone (NM)
Brian Pasko (NM)

JULY 2017 PUZZLE - "Tubular Bells"

Submitted by Dave Thomas

A windchime maker plans to cut a ten-foot length of conduit pipe into eight sections, such that the ratio of each piece to its longer neighbor is 4/5 = 0.8.

The July Bonus:What are the lengths of the longest and shortest pieces?

Hall of Fame (July Puzzle Solvers):

Keith Gilbert (NM)
Rocky S. Stone (NM)
Harold H. Gaines (KS)
Brian Pasko (NM)
Mike Arms (NM)
Terry Lauritsen (NM)

JUNE 2017 PUZZLE - "Gold for $100, Alex"

Created by Philip Kaplan, "Posers"

The June Bonus:Which is worth more, a carton full of $5 gold pieces or an identical carton half full of $10 gold pieces?

Hall of Fame (June Puzzle Solvers):

Earl Dombroski (NM)
Rocky S. Stone (NM)
Brian Pasko (NM)
Terry Lauritsen (NM)
Paul Braterman (UK)

MAY 2017 PUZZLE - "Those Quirky Quarks"

Submitted by Dave Thomas

According to the Standard Model of physics, a proton is composed of 3 quarks (two ups and one down), with a positive charge of 2/3 + 2/3 - 1/3 = 3/3 = 1. While a neutron is likewise made of 3 quarks (one up and two downs), it has a neutral charge of 2/3 - 1/3 – 1/3 = 0/3 = 0.

The May Bonus: The combined masses of the three quarks of a proton or neutron constitute what percentage of the rest mass of that proton or neutron?

• 1%
• 50%
• 97%
• 110%

Hall of Fame (May Puzzle Solvers):

Rocky S. Stone (NM)

Submitted by Dave Thomas

Consider the Pythagorean Scale, for which the frequency ratios to the lower C note are shown above. In the Well-Tempered Scale, on the other hand, the ratio of each note to the one preceding it is a constant 2^1/12.

The April Bonus: For the C-scale starting at 256 Hz, what note has the largest difference between well-tempered and Pythagorean scales? How many hertz off is it?

Hall of Fame (April Puzzle Solvers):

Rocky S. Stone (NM)
Gene Aronson (NM)
Harold H. Gaines (KS)
Alice Anderson(NM)

Rocky has made a sound file of the comparison, check it out here!

MARCH 2017 PUZZLE - "Isn't that Special!"

Submitted by Dave Thomas

A few weeks after the inauguaration of President John F. Kennedy, a math teacher at a small southwestern college told his students that they were living in a very special year. The professor said "The last time this happened, Billy the Kid was being tracked by Pat Garrett. The time before that, Suleiman II ended his reign as sultan of the Ottoman Empire."

The March Bonus: When was (or is) the next time this type of “Special Year” occurred (or will occur)?

Hall of Fame (March Puzzle Solvers):

Rocky S. Stone (NM)
Paul Braterman (UK)
Eric Hanczyc (WA)
Brian Pasko (NM)

FEBRUARY 2017 PUZZLE - "What's Your Sign?"

Submitted by Dave Thomas

Jim wants to make a political sign. At the art store, letters are priced according to a simple logical rule. Jim finds that he can purchase the letters to spell TRUMP for $11, PENCE for $12, and BANNON for $14.

The February Bonus: How much will Jim need to buy the letters for IMPEACH?

Hall of Fame (February Puzzle Solvers):

Paul Braterman (UK)
Rocky S. Stone (NM)
Eiichi Fukushima (NM)
Mike Arms (NM)
Eric Hanczyc (WA)
Keith Gilbert (NM)
Terry Lauritsen (NM)
Glenn Branch (CA)

JANUARY 2017 PUZZLE - "Keys to the Answer"

Submitted by Dave Thomas

Consider the calculator above. Assume that some non-zero number such as 1.0 has been placed into memory (MRC = memory recall). Now, consider the following sequence of calculator key strokes.

The February Bonus: If the sequence above is repeated many times, what is the eventual value of MRC, and how is that related to the first key in the sequence (7)?

Hall of Fame (January Puzzle Solvers):

Paul Braterman (UK)
Rocky S. Stone (NM)
Mike Arms (NM)
Eric Hanczyc (WA)

DECEMBER 2016 PUZZLE - "Electoral College Nightmare"

Submitted by Mike Arms

The December Bonus: For the 2016 US Presidential Election, what is the maximum difference in the Popular Vote that could still result in a losing Electoral Vote? Use these data (an Excel spreadsheet with these data is available at www.nmsr.org/electoral.xls).

Hall of Fame (December Puzzle Solvers):

Eric Hanczyc (WA)
Brian Pasko (NM)
Mike Arms (NM)

Click Here for December Puzzle Answer Page

NOVEMBER 2016 PUZZLE - "Math with Turkeys"

Submitted by Dave Thomas

Fred's turkey farm has a total of 100 Toms and Hens, having a net weight of 1,650 pounds. The distribution of turkey weights is remarkably uniform for each gender, and the typical Tom weighs twice as much as a typical Hen.

The November Bonus:
(A) What is the largest possible Hen’s weight? How many Toms and Hens are there for this weight?
(B) What is the largest Hen’s weight that is a round number of pounds? How many Toms and Hens?
(C) With an equal number of Toms and Hens, what is a typical Hen’s weight? How many Toms (= # Hens)?
(D) What is the smallest Hen’s weight that is a round number of pounds? How many Toms and Hens? And
(E) What is the smallest possible Hen’s weight? How many Toms and Hens?

Hall of Fame (November Puzzle Solvers):

Paul Braterman (UK)
Brian Pasko (NM)
Terry Lauritsen (NM)
Eric Hanczyc (WA)

OCTOBER 2016 PUZZLE - "Election Night Jitters"

Submitted by Dave Thomas

It’s election night, and candidate Shirley is running a tight race against candidate Ronald. Shirley has 55% of the vote, with 60% of the voters counted.

The October Bonus: What is the minimum percentage of votes Shirley needs from the remaining electorate in order for her to defeat Ronald?

Hall of Fame (October Puzzle Solvers):

Rocky S. Stone (NM)
Paul Braterman (UK)
Eric Hanczyc (WA)
Terry Lauritsen (NM)
Brian Pasko (NM)
Austin Moede (NM)
Alice Anderson(NM)

SEPTEMBER 2016 PUZZLE - "A Pair of Swingers"

Submitted by Dave Thomas

A rigid 12-inch ruler with a tiny hole at one end is hung on a nail, and allowed to swing back and forth. It is hung alongside four simple pendulums, of lengths 6, 8, 9 and 12 inches.

The September Bonus: Which one of the four simple pendula has the same period as the ruler??

Hall of Fame (September Puzzle Solvers):

Rocky S. Stone (NM)
Keith Gilbert (NM)
Terry Lauritsen (NM)
Eric Hanczyc (WA)
Alice Anderson(NM)

AUGUST 2016 PUZZLE - "Chilling by the Box"

Submitted by Dave Thomas

Given the solution to the July Bonus (probability that at least one adjacent pair of freeze pops has the same color, in a packet of 10 pops made with 6 colors, is ~ 0.806):

The August Bonus: In a typical box of eight packets (=80 freeze pops), what is the most likely number of packets (0-8) having at least one pair?

Hall of Fame (August Puzzle Solvers):

Paul Braterman (UK)
Brian Pasko (NM)
Alice Anderson(NM)
Eric Hanczyc (WA)

JULY 2016 PUZZLE - "Chilling for Summer"

Submitted by Dave Thomas

Freeze pops are a popular way to cool off. There are six different colors, and ten pops in a "rack".

The July Bonus: In a rack of ten freeze-pops, what is the probability of having at least one adjacent pair with the same color?

Hall of Fame (July Puzzle Solvers):

Paul Braterman (UK)
Eric Hanczyc (WA)
Alice Anderson(NM)
Keith Gilbert (NM)
Gene Aronson (NM)
Rocky S. Stone (NM)
Brian Pasko (NM)
Terry Lauritsen (NM)

JUNE 2016 PUZZLE - "The Corner Garden"

Submitted by Dave Thomas

Patsy wants to make a garden in the corner of her back yard, and has a fixed length L of border material to use. The corner walls bound two sides, as shown.

The June Bonus: Which design has more area for gardening, the triangle or the square?

Hall of Fame (June Puzzle Solvers):

Terry Lauritsen (NM)
Rocky S. Stone (NM)
Keith Gilbert (NM)
Brian Pasko (NM)
Eric Hanczyc (WA)
Alice Anderson(NM)

MAY 2016 PUZZLE - "The Envelope, Please?"

Submitted by Dave Thomas

You have a cannon, which can be controlled by its tilt angle and by the muzzle velocity v₀. Assume that the muzzle velocity v₀ is kept constant, and that the tilt angle can be varied, from shooting straight up, to shooting horizontally, as shown in the figure above.

The May Bonus:The thicker line in the figure above shows the envelope of all the positions the cannon can reach at constant muzzle velocity. What is the equation of this envelope?

Hall of Fame (May Puzzle Solvers):

Eric Hanczyc (WA)
Brian Pasko (NM)

APRIL 2016 PUZZLE - "Really Rolling Now!"

Submitted by Dave Thomas

Given the moment of inertia for a toilet paper roll from last month, suppose that two identical rolls are dropped at the same time. The first roll is dropped from a height h₁, and allowed to free-fall to the floor. The second roll is held onto by someone's hand at a height h₂, and unrolls as it falls.

The April Bonus:Assuming that the drop height is small enough that the roll's moment of inertia remains constant during the fall, what is the ratio of h₂ to h₁ to make the rolls land at the same instant?

Hall of Fame (April Puzzle Solvers):

Keith Gilbert (NM)
Eric Hanczyc (WA)
Brian Pasko (NM)

MARCH 2016 PUZZLE - "Rolling into π Day"

Submitted by Dave Thomas

Given these parameters for a roll of toilet paper: outer diameter 12 cm, inner diameter 6 cm, width 10cm, length 200 10cm x 10cm sheets, inner cardboard tube mass 4g, and roll (paper) mass 72g:

The March Bonus:(A) What is the sheet thickness, ΔT? (B) What is the moment of inertia of the roll, both initially, and as a function of radius r?

Hall of Fame (March Puzzle Solvers):

Eric Hanczyc (WA)
Keith Gilbert (NM)
Brian Pasko (NM)

FEBRUARY 2016 PUZZLE - "Gardening Time"

Submitted by Dave Thomas

You are busy in the garden, whipping up a batch of fertilizer for the plants. You need to measure exactly five gallons of water for the mix, but all you have at hand are two buckets (one has a three-gallon capacity, while the other holds seven-gallons). Neither bucket is graduated with gallon marks. You can get as much water as you you need from the hose, and any excess water can be used in the garden. Being clever, you quickly realize a method for using the two buckets to get exactly five gallons of water.

The February Bonus:How many gallons of water need to be supplied from the hose? And how many excess gallons of water will you pour into the garden?

Hall of Fame (Febuary Puzzle Solvers):

Keith Gilbert (NM)
Terry Lauritsen (NM)
Paul Braterman (UK)
Eric Hanczyc (WA)
Janell Woodbury (NM)
Alice Anderson(NM)
Rocky S. Stone (NM)
Ross Goeres (NM)
Brian Pasko (NM)

JANUARY 2016 PUZZLE - "Where's Papa?"

Submitted by Dave Thomas

On New Year's Eve of 2015, a certain woman was exactly 18 years older than her child. On New Year's Eve of 2018, she will be exactly nine times older than the child.

The January Bonus:On New Year's Eve 2015, where was the child's father?

Hall of Fame (January Puzzle Solvers):

Rocky S. Stone (NM)
Jackson Carmichael (Sydney, AUS)
Eric Hanczyc (WA)
Brian Pasko (NM)

DECEMBER 2015 PUZZLE - "The Crooked Waiter"

Submitted by Dave Thomas

The Three Stooges went to a cafe, and ordered a pizza for $15. They each contributed $5. The waiter took the money to the chef, who was a friend of the Stooges, and asked the waiter to return $5 to them.

The waiter was lazy and dishonest, however, and instead of splitting the $5 fairly between the three, he just gave them $1 each, and pocketed the remaining $2 for himself.

Now, Moe, Larry and Curly each had effectively paid $4, so the sum actually shelled out was $12. Along with the $2 in the waiter's pocket, everything totalled $14.

The December Bonus:Where did the other $1 go from the original $15?

Hall of Fame (December Puzzle Solvers):

Rocky S. Stone (NM)
Eric Hanczyc (WA)
Terry Lauritsen (NM)
Brian Pasko (NM)
Keith Gilbert (NM)

NOVEMBER 2015 PUZZLE - "To Tell The Truth..."

Submitted by Dave Thomas

Two types of intelligent bipedal organisms live on planet Blarnia: obligate liars and obligate truth tellers. The ambassador from Earth met with three Blarnians to negotiate a peace pact. One Blarnian spoke, but the ambassador didn't catch it. The second one remarked, "He said he was a liar." The third Blarnian yelled at the second, "You are lying!"

The November Bonus:Is the third Blarnian a liar or a truth teller?

Hall of Fame (November Puzzle Solvers):

Eric Hanczyc (WA)
Rocky S. Stone (NM)
Terry Lauritsen (NM)
Harold H. Gaines (KS)
Austin Moede (NM)
Brian Pasko (NM)

OCTOBER 2015 PUZZLE - "Drowning in Cicadas!"

Submitted by Dave Thomas

You're a naturalist trying to make sense out of cicada breeding patterns. The cicadas appear in different broods, and it appears that it's best for each brood if fewer other broods come out in their preferred breeding years. That minimizes the chances of genetic mixing between broods, and helps maintain brood lines.

The October Bonus:

• If red cicadas brood every 7 years, and green cicadas every 14 years, how many years will it be between years where both broods make their appearance?
• If red cicadas brood every 7 years, and green cicadas every 13 years, how many years will it be between years where both broods make their appearance?
• What does this suggest re optimal brood timings?

Hall of Fame (October Puzzle Solvers):

Alice Anderson(NM)
Brian Pasko (NM)
Keith Gilbert (NM)
Terry Lauritsen (NM)

SEPTEMBER 2015 PUZZLE - "Gee Whiz!"

Submitted by Dave Thomas

You're in a spaceship traveling at half of lightspeed relative to the Milky Way, and you need to reduce your speed to zero in order to disembark and visit Aunt Edna.

The August Bonus:

• Assuming that you can withstand the strain of 10 gees for some time, how long will it take to decelerate? (Assume one gee is 10 meters per second squared.)
• After deciding against torturing yourself for such a long time, you decide to take it a little easier, seven times easier to be precise. With a deceleration of 1.428 gees for some time, how long will it take to stop?
• Assuming that you can withstand the strain of 10 gees for 10 seconds, and that you'll need a full hour to recuperate from each grueling 10-second ordeal, what is your reduction in speed for one such event? And how many such efforts will it take to decelerate to zero meters/second?

Hall of Fame (September Puzzle Solvers):

Keith Gilbert (NM)
Terry Lauritsen (NM)
Eric Hanczyc (WA)
Brian Pasko (NM)
Eiichi Fukushima (NM)

AUGUST 2015 PUZZLE - "Traffic was Light"

Submitted by Dave Thomas

A driver on the interstate notices that, between every pair of adjacent mile markers, he encounters 30 cars in the oncoming lanes, on average.

The August Bonus:

• Assuming that cars in both directions are going the legal limit, what is the actual density of cars per mile for the oncoming lanes?
• A radio report informs the driver that that cars in the oncoming direction are going half of the legal limit, while cars going in his direction are doing the limit. What is the actual density of cars per mile for the oncoming lanes?
• A radio report informs the driver that that cars in the oncoming direction are going the legal limit, while cars going in his direction are doing half of the limit. What is the actual density of cars per mile for the oncoming lanes?

Hall of Fame (August Puzzle Solvers):

Terry Lauritsen (NM)
Brian Pasko (NM)
Keith Gilbert (NM)
Eric Hanczyc (WA)
Eiichi Fukushima (NM)

July 2015 PUZZLE - "Comin' Round the Track!"

Submitted by Dave Thomas

A train departs from New York City (NYC), heading toward Los Angeles (LA) at 100 mph. 3.5 hours later, a train departs from LA heading toward NYC at 200 mph. Assume there are 2000 miles of track between LA and NYC.

The July Bonus:(A) When do they meet?
(B) When they meet, which train is closer to NYC?

Hall of Fame (July Puzzle Solvers):

Gene Aronson (NM)
Paul Braterman (UK)
Keith Gilbert (NM)
Rocky S. Stone (NM)
Terry Lauritsen (NM)
Brian Pasko (NM)
Eiichi Fukushima (NM)
Alice Anderson(NM)
Eric Hanczyc (WA)
Mike Arms (NM)

June 2015 PUZZLE - "Winding Atomic Clocks"

Submitted by Dave Thomas

Assume a particular radioactive isotope (say, Uranium 238) has a "slow" half-life of TS (say, 4.48 billion years). Suppose that a sample has been collected from a given rock, and that the ratio of daughter isotope of lead (Pb206) to parent isotope (U238) in the sample is RS = 0.295. Likewise, a sample of a different radio-isotope (say, Uranium 235) with a "fast" half-life of TF (say, 704 million years) has also been collected from the same rock, and its ratio of daughter isotope (Pb207) to parent isotope (U235) is RF = 9.09.

Concordia/Discordia Chart: the horizontal axis is the fast daughter/parent ratio RF, and the vertical axis is the slow daughter/parent ratio RS.

The June Bonus:(A) In terms of the given halflife TH and current daughter/parent ratio R, what is the simplest, most elegant formula for predicting what the new value of the ratio will be after an additional passage of time of ΔT years? (Hint: the formula will have one positive exponent, no reciprocals, and just one pair of parentheses.)

(B) What will the ratios (RF, RS) = (9.09, 0.295) become after an additional time interval ΔT of 1 billion years?

(C) What will the ratios (RF, RS) = (18.18, 0.590) become after an additional time interval ΔT of 1 billion years?

Hall of Fame (June Puzzle Solvers):

Eric Hanczyc (WA)
Alice Anderson(NM)
Brian Pasko (NM)

May 2015 PUZZLE - "To Infinity, and Beyond!"

Submitted by Dave Thomas

For this puzzle, assume X is any non-zero number, and consider the iterative process in which X is replaced by 2 + 15/X.

The May Bonus:What does X converge to?

Hall of Fame (May Puzzle Solvers):

Paul Braterman (UK)
Eric Hanczyc (WA)
Keith Gilbert (NM)
Mike Arms (NM)
Brian Pasko (NM)
Ross Goeres (NM)
Alice Anderson(NM)

April 2015 PUZZLE - "Sustaining Livestock with the Joneses"

Submitted by Dave Thomas

Farmer Jones owns four times as many sheep as cattle. The grass on his farm is currently 12 inches high, and grows at a rate of two inches per day.

The grass on one acre of Farmer Jones' farm can support a dozen cattle for six days, accounting for daily growth. Alternatively, one acre of Farmer Jones' farm grass can support three dozen sheep for twelve days, again accounting for growth.

The April Bonus:What is the number of cattle and sheep per acre that will allow the land to support the livestock indefinitely? (Or at least, for the entire growing season?)

Hall of Fame (April Puzzle Solvers):

Paul Braterman (UK)
Terry Lauritsen (NM)
Eric Hanczyc (WA)
Mike Arms (NM)
Eiichi Fukushima (NM)
Alice Anderson(NM)

March 2015 PUZZLE - "Calling Dr. Venkman"

Submitted by Dave Thomas

A psychology class is testing their ESP abilities with Zener cards (five cards: circle, square, bacon, star, and cross).

The March Bonus:If each pair of students performs 25 trials, what is the minimum number of matches for the probability of guessing the cards to be less than one in a million?

Hall of Fame (March Puzzle Solvers):

Eric Hanczyc (WA)
Alice Anderson(NM)
Keith Gilbert (NM)
Brian Pasko (NM)
John Geohegan (NM)

February 2015 PUZZLE - "Even Money Powerball Bet?"

Submitted by Gene Aronson

To win the Powerball jackpot one must choose five different numbers from 1 to 59, plus the Powerball number from one of 35 numbers. The bet is two dollars. One can win in nine ways: the largest prize is for matching all 5 numbers and the Powerball, and is a variable amount. The other 8 amounts are fixed payouts. Here are all nine ways to win, and their prize amounts:

1. 5 numbers + Powerball (PB): JACKPOT
2. 5 numbers:$1,000,000
3. 4 numbers +PB:$10,000
4. 4 numbers:$100
5. 3 numbers +PB:$100
6. 3 numbers:$7
7. 2 numbers +PB:$7
8. 1 number +PB:$4
9. PB only: 4$

The February Bonus:What is the jackpot amount for an even bet (expected winnings = zero), for the situation in which (A) only the jackpot is considered, and the situation in which (B) all nine prizes are considered?

Hall of Fame (February Puzzle Solvers):

Eric Hanczyc (WA)
Brian Pasko* (NM)
Alice Anderson* (NM)
* Part (A)

January 2015 PUZZLE - "Moving Sidewalk"

Submitted by Dave Thomas

When his parent's holiday flight was cancelled because of snow, bored little Bobby decided to do some physics experiments on the Moving Sidewalk. He found that it took three minutes to go the length of the Sidewalk if he walked at his normal speed in the same direction as the Sidewalk was moving. He also found it took him six minutes to go the same length walking normally in the "wrong" direction.

The January Bonus:When the snow caused a blackout, the Moving Sidewalk stopped working. How many minutes did it take Bobby to walk the full length of the disabled Sidewalk?

Hall of Fame (January Puzzle Solvers):

Paul Braterman (UK)
Eiichi Fukushima (NM)
Mike Arms (NM)
Eric Hanczyc (WA)
Keith Gilbert (NM)
Gene Aronson (NM)
Terry Lauritsen (NM)
Harold H. Gaines (KS)
Rocky S. Stone (NM)
Allan Sauter (NM)
Alice Anderson (NM)

December 2014 PUZZLE - "I Just Need a Pair of Socks!"

Submitted by Dave Thomas

A frugal bachelor has exactly seven pairs of socks; four pairs are black, and three are white.

The December Bonus:If all 14 socks are lying around in random positions inside the bachelor's dryer, and he grabs the first two socks he can find in the dark, what is the probability he'll have (A) A black pair? (B) A white pair? (C) No pair at all?

Hall of Fame (December Puzzle Solvers):

Keith Gilbert (NM)
Mike Arms (NM)
Gene Aronson (NM)
Terry Lauritsen (NM)
Paul Braterman (UK)
Harold H. Gaines (KS)
Eric Hanczyc (WA)
Rocky S. Stone (NM)

November 2014 PUZZLE - "The Frugal Stalker"

Submitted by Dave Thomas

A certain stalker was tailing the target of his desires at the mall. As his prey entered several stores in the mall, the stalker would also enter the same store, but would always buy something to allay suspicion.

At the first store his victim entered, the stalker spent a third of the money he had on his person. At the second store, he spent a third of the remaining amount. And at the third store, he again spent a third of the remaining amount.

The November Bonus:If the stalker spent $38 all together, how much did he start with?

Hall of Fame (November Puzzle Solvers):

Keith Gilbert (NM)
Eiichi Fukushima (NM)
Paul Braterman (UK)
Rocky S. Stone (NM)
Beulah Woodfin (NM)
Harold H. Gaines (KS)
Mike Arms (NM)
Eric Hanczyc (WA)
Alice Anderson (NM)
Terry Lauritsen (NM)
Ross Goeres (NM)

October 2014 PUZZLE - "Who got my jersey?"

Submitted by Dave Thomas

James Randi, Michael Shermer, Richard Dawkins, and Neil deGrasse Tyson were all entered in a charity volleyball game. The sponsors printed up special jerseys with each of the four men's names. When Randi mischievously suggested that everyone wear another's jersey, all agreed with his marvelous prank.

The October Bonus:From the following information, deduce who was wearing each jersey:

• Randi wasn't wearing the jersey that belonged to Shermer.
• Dawkins didn't wear Randi's jersey, nor vice versa.
• Neil deGrasse Tyson got to serve ahead of the person wearing Randi's jersey.

Hall of Fame (October Puzzle Solvers):

Eric Hanczyc (WA)
Mike Arms (NM)
Rocky S. Stone (NM)
Eiichi Fukushima (NM)
Alice Anderson (NM)
Keith Gilbert (NM)
Ross Goeres (NM)

September 2014 PUZZLE - "Faster than g?"

Submitted by Dave Thomas

A hinged rod of length L is held at rest at an angle θ, and then released. At precisely the same moment, a steel ball is released from the same height as the top of the rod.

The September Bonus:If v_rod is the speed of the tip of the rod as it hits the flat table top, and v_ff is the speed of the free-falling steel ball as it impacts the same table top, what is the ratio of v_rod to v_ff ?

Hall of Fame (September Puzzle Solvers):

Keith Gilbert (NM)
Eric Hanczyc (WA)
Eiichi Fukushima (NM)

August 2014 PUZZLE - "The Physicist's Spouse"

Submitted by Dave Thomas

A physicist's spouse used a wheelchair, and this was firmly hooked to latches on the van's floor during excursions. The physicist wanted to minimize accelerations and decelerations while driving, as these were uncomfortable for his passenger. As they were cruising along at 12 meters/second (~27 mph), a red light turned on at the stop bar of the next intersection, a mere six meters away.

The August Bonus:Assuming the physicist applied constant brake pressure during the stop, and reduced the van's speed to zero just as it reached the stop bar, what was the time τ for the braking maneuver? And what was the constant acceleration a_o required?

• BONUS Bonus #2: Suppose the physicist used a linear deceleration rate, such that he covered the six meters in a time τ , starting at zero acceleration, and ending with zero speed, and acceleration a_o at the stop bar. What is the time τ for this braking maneuver, and what is the final acceleration a_o?
• BONUS Bonus #3: Suppose the physicist used a linear deceleration rate, such that he covered the six meters in a time τ , starting at acceleration a_o, and ending with zero speed and zero acceleration at the stop bar. What is the time τ for this braking maneuver, and what is the initial acceleration a_o?
• BONUS Bonus #4: In all three bonuses, the area under the acceleration curve from 0 to τ is the same for the two givens (6 meters to stop from an initial speed of 12 m/s). What is this area, and what does it signify? And, which of the three alternatives given is the best for the delicate spouse?

Hall of Fame (August Puzzle Solvers):

Keith Gilbert (NM)
Eric Hanczyc (WA)

July 2014 PUZZLE - "Gettin' Both Trucks Home"

Based on a True Story

University of Texas at Austin biologist David Hillis has a favorite "stuck in the middle of nowhere" story with a happy ending. He was out in his truck, hours away from Austin, when his alternator light came on. He watched his voltmeter drop until the truck stopped, hundreds of miles away from the closest place that could repair the alternator. Luckily for Hillis, his good friend Jim happened to drive by, and stopped to help. David Hillis could have ridden back to Austin with Jim, of course, but then his truck with its broken alternator and drained battery would still have been stuck in the middle of nowhere. Using one truck to tow the other was not feasible, either. However, the two clever men hit on a plan, and proceeded to return both trucks to Austin in a matter of just a few hours.

The July Bonus:How did David and Jim get both trucks back to Austin?

Hall of Fame (July Puzzle Solvers):

David B. Johnson (NM)
Terry Lauritsen (NM)
Alice Anderson * (NM)
Eric Hanczyc (WA)
Harold H. Gaines (KS)

June 2014 PUZZLE - "A Question of Time"

Courtesy Sam Loyd

The June Bonus:The hour and minute hands are at equal distance from the 6 hour, what time will it be exactly?

Hall of Fame (June Puzzle Solvers):

Mike Arms (NM)
Eric Hanczyc (WA)
Paul Braterman (UK)
Harold H. Gaines (KS)
Brian Pasko (NM)

May 2014 PUZZLE - "How Much Can JesĂşs Save?"

Submitted by Dave Thomas

A large grocery-store chain, Krikey's, has a promotion where their “Krikey Club” customers can get discounts on automobile fuel. For every dollar a customer spends at Krikey's, they get a point. When enough points are accumulated, they can be cashed in for gas discounts at the pump. The discounts come only in 10-cent intervals: 100 points gets the shopper a 10-cent discount per gallon of gas, 200 points would fetch a 20-cent discount, and so on up to 1000 points, and the maximum discount of a dollar per gallon. Discounts can not be used for more than 35 gallons at a time.

Points that are not used by the end of each calendar month are forfeited, and each month starts a clean slate for each customer.

Shopper JesĂşs Martinez spends the equivalent of 20 dollars per day at Krikeys every month. His old car's gas tank has a 24-gallon capacity, and he uses one gallon of gas per day. Assume the price of gas for a typical month is $3.33 per gallon, and that a month is 30 days long (for ease of calculations).

The May Bonus:What is the most JesĂşs can save? And how does he do it?

Hall of Fame (May Puzzle Solvers):

Keith Gilbert, $14.00 (NM)
Paul Braterman, $14.40 (UK)
Eric Hanczyc, $14.40 (WA)
Austin Moede (NM)

April 2014 PUZZLE - "Black and White Hats"

Courtesy mathisfun.com

Cannibals ambush a safari in the jungle and capture three men. The cannibals give the men a single chance to escape uneaten.

The captives are lined up in order of height, and are tied to stakes. The man in the rear can see the backs of his two friends, the man in the middle can see the back of the man in front, and the man in front cannot see anyone. The cannibals show the men five hats. Three of the hats are black and two of the hats are white.

Blindfolds are then placed over each man's eyes and a hat is placed on each man's head. The two hats left over are hidden. The blindfolds are then removed and it is said to the men that if one of them can guess what color hat he is wearing they can all leave unharmed.

The man in the rear who can see both of his friends' hats but not his own says, "I don't know". The middle man who can see the hat of the man in front, but not his own says, "I don't know". The front man who cannot see ANYBODY'S hat says "I know!"

The April Bonus:How did he know the color of his hat and what color was it?

Hall of Fame (April Puzzle Solvers):

Keith Gilbert (NM)
Rocky S. Stone (NM)
Brian Pasko (NM)
Mike Arms (NM)
Terry Lauritsen (NM)
Eric Hanczyc (WA)
Harold H. Gaines (KS)
Ken Lynch (TX)
Coffee Black (NM)

March 2014 PUZZLE - "An Engineer, A Physicist, And A Mathematician..."

Courtesy dailybrainteaser.blogspot.com

A farmer challenges an engineer, a physicist, and a mathematician to fence off the largest amount of area using the least amount of fence.

The engineer made his fence in a circle and said it was the most efficient.

The physicist made a fence all the way around the world, and said that fencing off one half of the Earth was the best possible outcome.

The mathematician laughed at the others and, with his design, beat them all.

The March Bonus:What was the mathematician's design?

Hall of Fame (March Puzzle Solvers):

Keith Gilbert (NM)
Rocky S. Stone (NM)
Paul Braterman (UK)
Terry Lauritsen (NM)
Eric Hanczyc (WA)

February 2014 PUZZLE - "The Seating Planner"

Submitted by Keith Gilbert

Three couples are to be seated at a circular table surrounded by chairs numbered # 1-6. The Host has each person draw a random number, 1 through 6, and sit in that seat.

The February Bonus:What is the chance that no one will sit next to their "significant other" ?

Hall of Fame (February Puzzle Solvers):

John Geohegan (NM)
Eric Hanczyc (WA)
Kat Schroeder (NM)
Mike Arms (NM)
Brian Pasko (NM)

January 2014 PUZZLE - "What Am I?"

Traditional

Always old, sometimes new, never sad, sometimes blue. Never empty, sometimes full, never pushes, always pulls.

The January Bonus:What Am I?

Hall of Fame (January Puzzle Solvers):

Rocky S. Stone (NM)
Mike Arms (NM)
Eric Hanczyc (WA)
Harold H. Gaines (KS)
Ross Goeres (NM)
Terry Lauritsen (NM)

December 2013 PUZZLE - "Plumb Strange"

Submitted by Dave Thomas

Consider an irregular flat surface such as pictured below. To find the center of mass of the object, three plumb lines have been drawn, but the measurements weren't exact, and the three lines do not intersect at a single point. Instead, the three intersections lines form a triangle as shown.

The December Bonus:Assuming that the probability of finding the true center of mass on either side of each line is ½, what is the probability that the true center of mass is actually located within the triangle?

Hall of Fame (December Puzzle Solvers):

Paul Braterman (UK), correct answer: UNDETERMINED
Dave Thomas (NM) (1/8)
Harold H. Gaines (KS) (1/8)
Ross Goeres (NM) (1/8)
Keith Gilbert (NM) (7/8)
Eric Hanczyc (WA) (7/8)
Rocky S. Stone (NM) (1/4)

November 2013 PUZZLE - "Highway 119,163 Revisited"

Submitted by Dave Thomas

The November Bonus: A commuter who dabbles in mathematics has observed that, when he travels north on his preferred interstate highway, the difference between the highway's mile markers and his own car's odometer is a constant. (Actually, this 'constant' can change drastically for different interstate trips, and even varies a bit during a single trip, but let's assume it's a constant for any given trip.) He has also observed that, when he's on the same freeway southbound, the sum of the highway's mile markers and his own car's odometer is a (different) constant.

As our commuter leaves a small town and enters the interstate, he notes that his constant for this trip is 119,163, while if he had gone the other direction, his constant would have been 118,799.

The November Bonus:

1. What is the interstate mile marker at this intersection?
2. What is the commuter's odometer reading here?
3. Which direction is he going on the freeway?

Hall of Fame (November Puzzle Solvers):

Harold H. Gaines (KS)
Eric Hanczyc (WA)
Mike Arms (NM)
Ross Goeres (NM)
Keith Gilbert (NM)
Brian Pasko (NM)
Rocky S. Stone (NM)

October 2013 PUZZLE - "A Nine Digit Bonus"

Submitted by John Geohegan

Chapter 16 of Martin Gardner’s Wheels, Life and Other Mathematical Amusements shows how the nine non-zero digits may be arranged in two groups so that 158x23 = 79x46, which gives the product of 3634. He tells us there are two more solutions that arrange the same nine digits in the same pattern(three digits times two digits equals two digits times two digits), with the two products both being larger than 3634.

The October Bonus:What are they? And can you find them without using a computer?

Hall of Fame (October Puzzle Solvers):

Ross Goeres (NM)
Eric Hanczyc (WA)
Harold H. Gaines (KS)
Steve Hagen (SD)
Rocky S. Stone (NM)

September 2013 PUZZLE - "What is her name?"

Submitted by Dave Thomas

Consider this equation:

5e^3x - 3e^5x + 162.0900441 = 0

The September Bonus: Solve for x.

The September BONUS Bonus: If the first seven digits of x after the decimal were someone's phone number, what is her name?

Hall of Fame (September Puzzle Solvers):

Gene Aronson (NM)
Eric Hanczyc (WA)
Paul Moore (NM)
John Geohegan (NM)
Mike Arms (NM)
Brian Pasko (NM)
Ross Goeres (NM)
Harold H. Gaines (KS)
Keith Gilbert (NM)

August 2013 PUZZLE - "The Sock Drawer"

Submitted by John Geohegan

Here is the first problem from Frederick Mosteller's book, Fifty Challenging Problems in Probability, with Solutions:

A drawer contains red socks and black socks. When two socks are drawn at random, the probability that both are red is 1/2.

The August Bonus: How small can the number of socks in the drawer be?

The August BONUS Bonus: How small can the number of socks in the drawer be, if the number of black socks is even? ?

Hall of Fame (August Puzzle Solvers):

Keith Gilbert (NM)
Paul Braterman (UK)
Gene Aronson (NM)
Ross Goeres (NM)
Mike Arms (NM)
Harold H. Gaines (KS)
Rocky S. Stone (NM)
Terry Lauritsen (NM)
Eric Hanczyc (WA)

July 2013 PUZZLE - "Rock,Paper,Scissors,Lizard,Spock"

Submitted by Dave Thomas

Physicist Leonard thinks that traditional "Rock, Paper, Scissors" produces too many ties, and has proposed expanding the popular hand game to "Rock, Paper, Scissors, Lizard, Spock." The expanded rules are: Scissors cuts Paper, Paper covers Rock, Rock crushes Lizard, Lizard poisons Spock, Spock smashes Scissors, Scissors decapitates Lizard, Lizard eats Paper, Paper disproves Spock, Spock vaporizes Rock, and (as it has always) Rock crushes Scissors.

The July Bonus: If the game is played 900 times, with a good random number generator to pick the choices for both players, how many fewer ties will there be with "Rock, Paper, Scissors, Lizard, Spock" than with the old "Rock, Paper, Scissors?

Hall of Fame (July Puzzle Solvers):

Paul Braterman (UK)
Rocky S. Stone (NM)
Keith Gilbert (NM)
Eric Hanczyc (WA)
Ross Goeres (NM)
Harold H. Gaines (KS)
Brian Pasko (NM)
Mike Arms (NM)

June 2013 PUZZLE - "Felix's Selection..."

Submitted by Dave Thomas

Felix Unger, known for his fastidiousness and attention to detail, needs three pens for a task. Roomie Oscar Madison's pen jar has a jumble of 30 pens – eleven red, nine brown, six black, and four violet.

The June Bonus:If pens are chosen without looking, what is the minimum number of pens that Felix must withdraw from the jar to ensure having three of the same color?

Hall of Fame (June Puzzle Solvers):

Rocky S. Stone (NM)
Keith Gilbert (NM)
Mike Arms (NM)
Terry Lauritsen (NM)
Harold H. Gaines (KS)
Eric Hanczyc (WA)
Brian Pasko (NM)
Ross Goeres (NM)

May 2013 PUZZLE - "And the Winner Is..."

Submitted by Dave Thomas

The May Bonus:What is the next number in the following sequence?
0, 0, 14, 60, 156, 320, 570, 924,...

Hall of Fame (May Puzzle Solvers):

Rocky S. Stone (NM)
Eric Hanczyc (WA)
Harold H. Gaines (KS)
Peggy Mavretich(NM)
Mike Arms (NM)

April 2013 PUZZLE - "ROLL DEM BONES"

Submitted by Dave Thomas

When you roll a pair of six-sided dice, the most likely result is 7, with a probability of 6/36 = 1/6.

The April Bonus:What is the likeliest value and corresponding probability for rolling four dice? And for rolling six dice?

Hall of Fame (April Puzzle Solvers):

Paul Braterman (UK)*
Keith Gilbert (NM)
Terry Lauritsen (NM)*
John Geohegan (NM)*
Harold H. Gaines (KS)
Eric Hanczyc (WA)
Rocky S. Stone (NM)
*: Partial Credit

March 2013 PUZZLE - "CIRCULAR REASONING"

Submitted by John Geohegan

A circular table is pushed against two walls at right angles to each other.

The March Bonus: If a spot on the rim is eight inches from one wall and nine inches from the other, what is the diameter of the table?

Hall of Fame (March Puzzle Solvers):

Keith Gilbert (NM)*
Mary LaPoint (NM)
Eric Hanczyc (WA)
Harold H. Gaines (KS)*
Paul Braterman (UK)*
Mike Arms (NM)
Terry Lauritsen (NM)*
Rocky S. Stone (NM)

February 2013 PUZZLE - "A SIMPLE MULTIPLICATION"

Submitted by John Geohegan

This problem is intended as a warm-up for the upcoming March meeting, showing how hard it is to factor the product of a simple multiplication.

The February Bonus: What two prime numbers multiplied together equal 70,531?

Hall of Fame (February Puzzle Solvers):

Rocky S. Stone (NM)
Keith Gilbert (NM)
Mike Arms (NM)
Mary LaPoint (NM)
Eric Hanczyc (WA)

January 2013 PUZZLE - "Nyuk Nyuk - A Half a Loaf is Better than What?"

Submitted by Dave Thomas

The Three Stooges walked into a Deli to buy some bread. Moe bought half the bread remaining on the shelves, and half of a loaf more. Larry and Curly each did the same. After they had left, the baker promptly closed the Deli, as his bread was sold out. Surprisingly, the baker didn't need to cut even one loaf.

The January Bonus: how many loaves were on the shelves when the Stooges came in?

Hall of Fame (January Puzzle Solvers):

Paul Braterman (UK)
Keith Gilbert (NM)
Mike Arms (NM)
Bob Schmidt (NM)
Terry Lauritsen (NM)
Eric Hanczyc (WA)
Steve's brother-in-law (IL)
Harold H. Gaines (KS)
Mary LaPoint (NM)
Ken Lynch (TX)
Rocky S. Stone (NM)

December 2012 PUZZLE - "Couch Potato"

Submitted by Dave Thomas

Couch Potato Larry doesn't like to watch commercials, so if a show he is watching goes to commercial, he'll flip to the other network to watch actual programming. We are given this inside information: there are only two television networks, TEE and VEE, and each runs shows for 2/3 of the time, and commercials for 1/3 of the time. So, there are three ways things can turn out at any specific time:

1. Either both TEE and VEE are showing commercials;
2. One network is showing a commercial, while the other is showing real programming;
3. Both stations are showing real programming.

The December Bonus: in the long run, which scenario (1,2, or 3) is most likely? And which is least likely?

Hall of Fame (December Puzzle Solvers):

Keith Gilbert (NM)
Paul Braterman (UK)
Steve's brother-in-law (IL)
Mike Arms (NM)
Rocky S. Stone (NM)
Eric Hanczyc (WA)
Terry Lauritsen (NM)
Harold H. Gaines (KS)

November 2012 PUZZLE - "Langford's Problem"

Submitted by John Geohegan

The November Bonus
In Martin Gardner's Magic Show, he describes Langford's Problem, which is to arrange four pairs of cards: two aces, two deuces, two threes, and two fours side by side in a row so that one card separates the aces, two cards separate the deuces and so on. What is the solution? Apparently there are no solutions with five or six pairs of cards, but there are 26 solutions with seven pairs.

Hall of Fame (November Puzzle Solvers):

Keith Gilbert (NM)
Eric Hanczyc (WA)
Mike Arms (NM)
Rocky S. Stone (NM)
Harold H. Gaines (KS)
Steve's brother-in-law

October 2012 PUZZLE - "Repeating Decimal"

Submitted by Dave Thomas

The October Bonus
Find the reduced fraction that is equal to 0.967032967032967032... .

Hall of Fame (October Puzzle Solvers):

Keith Gilbert (NM)
Eric Hanczyc (WA)
Mike Arms (NM)
Harold H. Gaines (KS)
Austin Moede* (NM)
Roy Thearle (UK)
Rocky S. Stone (NM)

September 2012 PUZZLE - "The Speed of Shadow"

Submitted by John Geohegan

Here's a problem from Martin Gardner's Mathematical Carnival which I haven't yet solved. “A man walking at night along a sidewalk at a constant speed passes a street light.”

The September Bonus
As his shadow lengthens, does the top of the shadow move faster or slower or at the same rate as it did when it was shorter?

Hall of Fame (September Puzzle Solvers):

Keith Gilbert (NM)
Paul S. Braterman (UK)
Brian Pasko (NM)
Rocky S. Stone (NM)
Harold H. Gaines (KS)

August 2012 PUZZLE - "Triangular Solitaire"

Submitted by John Geohegan

Starting with ten bowling pins in the usual position, and then removing the #2 pin, show how to remove the remaining nine pins by jumping, checkers style, over a pin to be removed and into a vacant position. Eight pins may be removed in six moves as follows, leaving only one pin standing:

1. 7-2, Jumping from the #7 position over the pin on spot #4 into the vacant #2 spot, removing the pin at spot #4.
2. 9-7, removing the pin at spot #8.
3. 1-4, removing the pin at spot #2.
4. 7-2, removing the pin at spot #4.
5. 6-4, 4-1, 1-6, a triple jump removing pins at spots #5, #2, and #3.
6. 10-3, removing the pin at spot #6.

The August Bonus
Starting with a vacancy at spot #3, show how to remove eight pins in five jumps, leaving only one pin standing.

Hall of Fame (August Puzzle Solvers):

Rocky S. Stone (NM)
Keith Gilbert (NM)
Eric Hanczyc (WA)

JULY 2012 PUZZLE - "That Old, Lazy River"

Courtesy “200 Puzzling Physics Problems” by Gnädig, Honyek and Riley, 2001

A boat can travel at a speed of 3m/sec on still water. A boatman wants to cross a river whilst covering the shortest possible distance.

The July Bonus
In what direction should he row with respect to the bank if the speed of the water is (A) 2 m/sec, (B) 4 m/sec.? Assume that the speed of the water is the same everywhere.

Hall of Fame (July Puzzle Solvers):

Rocky S. Stone (NM)
Keith Gilbert (NM)
Eric Hanczyc (WA)

Hall of Honorable Mention (July Puzzle Partial Solvers):

Austin Moede (NM)

JUNE 2012 PUZZLE - "Paging Dr. Bayes..."

Submitted by Dave Thomas

In a large hospital, Dr. Bayes was wondering about the accuracy of a certain test for the dreaded Cambrian Protoplasmic Ailment (CPA), which affects 1% of the general population. The test itself is touted as being 88% accurate (this is the probability that people suffering the disease get a positive test result). Bayes finds additional information showing that the false positive rate for the test is 8%.

The June Bonus
(A) If patient John Doe gets a positive test result, what is the probability he has CPA? (B) If patient John Doe gets a negative test result, what is the probability he has CPA?

Hall of Fame (June Puzzle Solvers):

Eric Hanczyc (WA)
Keith Gilbert (NM)
Austin Moede (NM)

MAY 2012 PUZZLE - "An N-Step Program"

Submitted by Dave Thomas

There is a long escalator of N steps in height. Young Albert likes to time how long it takes to get to the top of the escalator when he runs different numbers of steps before riding the rest of the way.

Albert finds that, if he runs 14 steps, then it takes an additional 42 seconds to reach the top. And, if he runs 24 steps, it only takes 27 seconds more to reach the top.

The May Bonus
(A) How many steps does the escalator have?
(B) How fast is the escalator moving?
(C) How long would it take to ride the whole way (no running)?
(D) What is Albert's maximum running speed with respect to the escalator?

Hall of Fame (May Puzzle Solvers):

Keith Gilbert (NM)
Eric Hanczyc (WA)
Rocky S. Stone (NM)

APRIL 2012 PUZZLE - "The Triangular Pins"

Submitted by John Geohegan

In bowling, how many of the ten pins can be placed simultaneously on their spots without forming an equilateral triangle? Thus pins 1, 7, and 10 would form an equilateral triangle, as would pins 6,9, and 10.

Hall of Fame (April Puzzle Solvers):
Keith Gilbert (NM)
Terry Lauritsen (NM)
Rocky S. Stone (NM)
Eric Hanczyc (WA)
Ken Lynch (TX)

MARCH 2012 PUZZLE - "The 15-minute Egg"

Submitted by John Geohegan

Here's a problem from Martin Gardner's "Mathematical Circus" which he credited to Carl Fulves, who wrote many books on magic: "With a 7-minute hourglass and an 11-minute hourglass, what is the quickest way to time the boiling of an egg for 15 minutes?"

Hall of Fame (March Puzzle Solvers):
Keith Gilbert (NM)
Eric Hanczyc (WA)
Harold H. Gaines (KS)
Rocky S. Stone (NM)
Mike Arms (NM)
Terry Lauritsen (NM)

FEBRUARY 2012 PUZZLE - "Something is Askew..."

Submitted by Dave Thomas

Consider these pictures, taken from a moving car with an i-phone's camera. In these images, the telephone pole, picket fence, houses, etc. are all actually vertical, and the tilt is only an artifact of the car's motion. Note that the skewing effect depends on distance. All the images were taken from a car moving at ~ 55 mph (to the left). The effect is strongest for the closest objects.

Images courtesy Yvonne Ly.

The February Bonus:

If the camera is pointed at a right angle to the line of travel, and if the telephone pole in the first image is about 12 feet away from the camera's line of travel, and if the car is moving at about 55 mph, then the pole will appear to be tilted by about 15 degrees.
Given all that, how long does it take for this camera to save an image?

Hall of Fame (February Puzzle Solvers):
Rocky S. Stone (NM)
John Geohegan (NM)

JANUARY 2012 PUZZLE - "Bungee Fever"

Courtesy "200 Puzzling Physics Problems" by Gnädig, Honyek and Riley, 2001.

A man of height h₀ = 2m is bungee jumping from a platform situated at a height h = 25m above a lake. One end of an elastic Bungee cord is attached to his foot, and the other end is fixed to the platform. The man drops from rest in a vertical (head-down for convenience) position.

The length and elastic properties of the bungee cord (treat it like a classical spring with constant K) are such that the man's speed is zero at the instant his head just reaches the surface of the lake. Eventually, the jumper ends up dangling with his head 8 meters above the water.

The January Bonus:

• (A) What is the unstretched length of the Bungee cord?
• (B) What was the jumper's maximum speed?
• (C) What was the maximum tension in the Bungee cord?
• (D) What was the jumper's peak acceleration?

Hall of Fame (January Puzzle Solvers):
Keith Gilbert (NM)
John Geohegan (NM)

DECEMBER '11 PUZZLE - "Honey, I Shrank the Solar System FOLLOWUP"

Submitted by Dave Thomas

If the solar system were proportionally reduced so that the average distance between the Sun and the Earth were 1 meter, and the density of matter was unchanged, how far away would a 60-kg observer have to be for his or her gravitational effect on the tiny Earth to be just equal to the tiny sun's effect?

Assume no other matter is nearby.

Hall of Fame (December Puzzle Solvers):
John Geohegan (NM)
Keith Gilbert (NM)
Rocky S. Stone (NM)

NOVEMBER '11 PUZZLE - "Honey, I Shrank the Solar System..."

Courtesy "200 Puzzling Physics Problems" by Gnädig, Honyek and Riley, 2001.

IF the solar system were proportionally reduced so that the average distance between the Sun and the Earth were 1 meter, how long would a year be? Take the density of matter to be unchanged.

The November Bonus: How long would a year be?

Hall of Fame (November Puzzle Solvers):
Paul Braterman (UK)
Rocky S. Stone (NM)
Keith Gilbert (NM)
Eric Hanczyc (WA)

OCTOBER '11 PUZZLE - "A Certain Height"

Submitted by Christopher Allan

• If you take a lead ball up a ladder and let it go, it falls to the ground.
• If you take it up a tall building and let go, it still falls to the ground.
• If you take it up in a plane and drop it, it falls to the ground, in due course.
• If you take it up to a certain height and let it go, it remains suspended at that point.

The October Bonus: What height is it?

Hall of Fame (October Puzzle Solvers):
Rocky S. Stone (NM)
Eric Hanczyc (WA)
Harold H. Gaines (KS)
Ross Goeres (NM)

SEPTEMBER '11 PUZZLE - "Remainder of One"

Adapted from Intriguing Mathematical Problems by Oswald Jacoby, with W. H. Benson.

The September Bonus: What is the smallest number divisible by 13 which, divided by any of the numbers 2 to 12 inclusive, leaves a remainder of 1?

Hall of Fame (September Puzzle Solvers):
Harold H. Gaines (KS)
Eric Hanczyc (WA)
Mike Arms (NM)
Ross Goeres (NM)
Keith Gilbert (NM)
Rocky S. Stone (NM)

AUGUST '11 PUZZLE - "The Pop Quiz"

Submitted by Dave Thomas.

The August Bonus: Is this equation valid? Why?

Hall of Fame (August Puzzle Solvers):
Paul Braterman (UK)
John Geohegan (NM)
Keith Gilbert (NM)
Ross Goeres (NM)
Eric Hanczyc (WA)
Rocky S. Stone (NM)
Frank Thomas (CA)

JULY '11 PUZZLE - "The Painted Cubes"

Submitted by John Geohegan.

From my father's collection: A number of identical white cubes are to have painted on each face a line through the center of the face and parallel to one pair of edges. Thus the line on any face might be oriented in either of two directions. How many cubes can be painted in this way so as to be distinguishable from one another? Two patterns are distinguishable if and only if one is not a rotation of the other.

The July Bonus: How many cubes?

Hall of Fame (July Puzzle Solvers):
Rocky S. Stone (NM)

JUNE '11 PUZZLE - "Across the River Wide"

Submitted by Christopher Allan, UK.

Two boats start off to cross a river from opposite sides at the same time. They meet at a point 720 yards from the nearest shore, reach the opposite bank, then set off in return, meeting again 400 yards from the other shore. Constant speeds again.

The June Bonus: How wide is the river?

Hall of Fame (June Puzzle Solvers):
Keith Gilbert (NM)
Brian Pasko (NM)
Eric Hanczyc (WA)
Frank Thomas (CA)
Harold H. Gaines (KS)
Ross Goeres (NM)
Rocky S. Stone (NM)

MAY '11 PUZZLE - "The Advancing Column"

Submitted by Christopher Allan, UK.

A column on the march is 4 miles long. A man at the rear decides to run ahead to the front, speak briefly to someone at the front, and run back to the rear. During this time the column has advanced 3 miles. Assume speeds constant and instantaneous turning.

The April Bonus: How far did the runner travel?

Hall of Fame (May Puzzle Solvers):
Paul Braterman (UK)
Eric Hanczyc (WA)
Keith Gilbert (NM)
Ross Goeres (NM)

APRIL '11 PUZZLE - "The Erudite Bookworm"

Adapted from Intriguing Mathematical Problems by Oswald Jacoby, with W. H. Benson.

The bookworm is a staple character in puzzle literature. Ours, finding himself in a library in which the sets of books were placed in the usual sequence, decided to sample some Shakespeare from a two-volume edition on a bottom shelf. Beginning with the Foreword of Volume 1, and boring through in a straight line to the last page of Volume 2, the bookworm made his way at the rate of one inch every four days. If each cover is an eight of an inch thick, and if each volume measures three inches in thickness:

The April Bonus: How long will it take the Erudite Bookworm to digest his way through Shakespeare?

Hall of Fame (April Puzzle Solvers):

Rocky Stone (NM)
Kim Johnson (NM)
Keith Gilbert (NM)
Harold H. Gaines (KS)
Ross Goeres (NM)
Peter Lundman (NM)

MARCH '11 PUZZLE - "Look, Ma – No Hands!"

Courtesy John Geohegan.

The January Bonus problem about determining the direction of bicycle travel was fascinating. Maybe our readers will find similar satisfaction in the following bicycle problems.
1. Is the ability to ride "no hands" the result of fork geometry or gyroscopic forces?
2. If you're riding "no hands" and you push forward gently on the right handlebar, which way will the bike turn?
3. If you have a friend keep a stationary riderless bicycle upright and you then reach down and push the lower pedal to the rear, which way will the bicycle move? Which way will the pedals move?
4. Since the left pedal rotates clockwise relative to the crank, why is a lefthand thread used on the pedal spindle?

Hall of Fame (March Puzzle Solvers):

Rocky Stone (NM)
Ross Goeres (NM)

TO SEE HIDDEN SOLUTION TO MARCH PUZZLE: Select text from "HERE" to

1. Is the ability to ride "no hands" the result of fork geometry or gyroscopic forces? Ans. Fork geometry. This question was answered most persuasively by David E.H. Jones in the April 1970 issue of Physics Today, reprinted in Sept. 2006, showing the gyroscopic forces had very little effect but the fork design could result in ultra stability.

2. If you're riding "no hands" and you push forward gently on the right handlebar, which way will the bike turn? Ans. To the right. Due to counter-steering my bike swerves very slightly to the left and then steers into a right-hand turn with no force from my left hand.

3. If you have a friend keep a stationary riderless bicycle upright and you then reach down and push the lower pedal to the rear, which way will the bicycle move? Which way will the pedals move? Ans. The bicycle will roll backward and the pedals will rotate backwards in apparent defiance of the direction you're pushing. It's worth doing the experiment with a real bicycle.

4. Since the left pedal rotates clockwise relative to the crank, why is a left-hand thread used on the pedal spindle? Ans. Due to the downward force on the pedal, the pedal spindle in contact with the internal threads of the crank is given a counter-clockwise torque which would loosen a right-hand. thread.

"THERE"

FEBRUARY '11 PUZZLE - "Kid Conundrum!"

Courtesy Brain Teasers Forum, BrainDen.com.

Two friends are chatting:
- Peter, how old are your children?
- Well Thomas, there are three of them and the product of their ages is 36.
- That is not enough ...
- The sum of their ages is exactly the number of beers we have drunk today.
- That is still not enough.
- OK, the last thing is that my oldest child wears a red hat.

The February Bonus: How old were each of Peter's children?

Hall of Fame (February Puzzle Solvers):

Rocky Stone (NM)
Paul Braterman (UK)
Keith Gilbert (NM)
Eric Hanczyc (WA)
Ross Goeres (NM)
Harold H. Gaines (KS)
Mike Arms (NM)

JANUARY '11 PUZZLE - "Follow That Bike!"

Courtesy Peter Doyle, Dartmouth.

C. Dennis Thron has called attention to the following passage from The Adventure of the Priory School, by Sir Arthur Conan Doyle:

"This track, as you perceive, was made by a rider who was going from the direction of the school."
"Or towards it?"
"No, no, my dear Watson. The more deeply sunk impression is, of course, the hind wheel, upon which the weight rests. You perceive several places where it has passed across and obliterated the more shallow mark of the front one. It was undoubtedly heading away from the school."

The January Bonus: (A) Does Holmes know what he's talking about?
(B) Try to determine the direction of travel for the idealized bike tracks in this diagram.

Hall of Fame (January Puzzle Solvers):

John Geohegan (NM)
Eric Hanczyc (WA)
Honorable Mention: Rocky S. Stone (NM)

DECEMBER '10 PUZZLE - "The Three-Pointed Problem"

Submitted by Dave Thomas.

Consider these nine equilateral triangles; centroids are shown for the three non-shaded triangles.

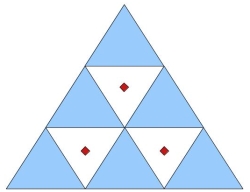
The December Bonus: What is the ratio of areas of the triangle whose vertices are the three centroids shown, to any individual triangle? And, to the large triangle composed of nine small ones?

Hall of Fame (December Puzzle Solvers):

Eric Hanczyc (WA)
Rocky S. Stone (NM)
Keith Gilbert (NM)
Ross Goeres (NM)
Harold H. Gaines (KS)
Mike Arms (NM)

NOVEMBER '10 PUZZLE - "A PLAYGROUND RACE"

Submitted by John Geohegan.

A playground race will be won by the runner who most quickly runs from a starting pole to a long North-South wall, touching any point along the wall, and then runs to a finishing pole which is 90 feet due northeast of the starting pole. If the wall is 70 feet west of the starting pole, what is the shortest distance the winner can run?

Hall of Fame (November Puzzle Solvers):

Harold Gaines (KS)
Rocky S. Stone (NM)
Ross Goeres (NM)
Keith Gilbert (NM)

OCTOBER '10 PUZZLE - "Binary Bemusement"

Submitted by Dave Thomas.

Just over 50 light years from Earth, the two small stars comprising Castor C orbit each other with a period of 0.8 days, orbital speeds of 0.0004c (c=lightspeed), and a separation of about 1.39x10-7 lightyears (~1.6 million miles). Assume that the orbital plane of Castor C contains/is parallel to the line-of-sight from Earth. If Einstein had been wrong – if the light emitted by these binary stars did indeed depend on the motion of the source, and moves toward Earth at speeds between 0.9996 and 1.0004c -- then, what would an Earth-based observer see upon training a telescope on Castor C?
(A) The two stars, both bright points moving in oscillating paths along opposite directions, with a period of just over 19 hours.
(B) Both stars, producing a continuous path of light, perhaps a very elongated ellipse.
(C) Two "necklaces" with dozens of stars in each, moving in the same direction, with stars appearing as pairs on one side of the necklace, and disappearing as pairs on the other side.
BONUS BONUS: How large a telescope (Newton reflector diameter) would be required to actually resolve the separate images of the binary stars?

Hall of Fame (October Puzzle Solvers):

Keith Gilbert (NM)

SEPTEMBER '10 PUZZLE - "Series-ously Infinite!"

Submitted by Dave Thomas.

Consider the replacement X ? 1 + 1/X. (A) If the first X is 1, what does the series (1, 2, 3/2, 5/3, …) converge to? (B) What do you get if you square the answer for (A), then subtract one? (C) What mathematician am I thinking of?

Hall of Fame (September Puzzle Solvers):

Paul Braterman (UK)
Mike Arms (NM)
Harold H. Gaines (KS)
Eric Hanczyc (WA)
Ross Goeres (NM)

AUGUST '10 PUZZLE - "Super-Size Me!"

Submitted by John Geohegan.

Use the nine digits, 1,2,3,4,5,6,7,8,and 9, each exactly once to form two numbers which give a maximum when multiplied together. Thus, 7128 times 56934 uses the digits properly but doesn't give the maximum possible product.

The August Bonus: What two numbers yield the maximum product?

Hall of Fame (August Puzzle Solvers):

Mike Arms(NM)
Ross Goeres (NM)
Michael Terrell (NM)

JULY '10 PUZZLE - "All Downhill From Here"

Submitted by Dave Thomas.

A physicist notes that two solid spheres of different sizes roll down a ramp at the same speeds, and similarly for two thin-walled hollow spheres, two solid cylinders, and two thin-walled hollow cylinders. When he races different shapes, however (such as a thin-walled hollow cylinder versus a solid sphere), they run at different speeds.

The July Bonus: If some solid and thin-walled hollow cylinders and spheres (four objects all together) are released simultaneously at the top of the ramp, in what order will they arrive at the bottom?

Hall of Fame (July Puzzle Solvers):

Mike Arms (NM)
Keith Gilbert (NM)
Harold H. Gaines (KS)
Ross Goeres (NM)

JUNE '10 PUZZLE - "MISSPELLING MISSISSIPPI"

Submitted by John Geohegan.

Of all the ways of arranging all eleven letters of Mississippi, how many ways don't spell Mississippi?

Hall of Fame (June Puzzle Solvers):

Keith Gilbert (NM)
Mike Arms (NM)
Rocky S. Stone (NM)
Ross Goeres (NM)

MAY '10 PUZZLE - "The Weightless Scale"

Submitted by Dave Thomas.

On the left, the massless scale hanging from the ceiling will read "10 kg" for the 10-kg mass shown. On the right is a system with a similar hanging scale, supporting a massless pulley and a 10-kg mass, with one rope anchored to the floor, as shown.

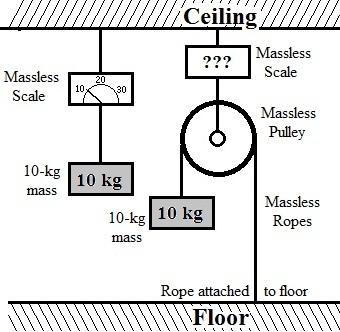
The May Puzzle: What is the reading on the Weightless Scale above the pulley?.

Hall of Fame (May Puzzle Solvers):

Paul S. Braterman (UK)
Ken Hessel (NM)
Harold H. Gaines (KS)
Mike Arms (NM)
Keith Gilbert (NM)
Ross Goeres (NM)

APRIL '10 PUZZLE - "Finding Inner Balance"

Submitted by Dave Thomas.

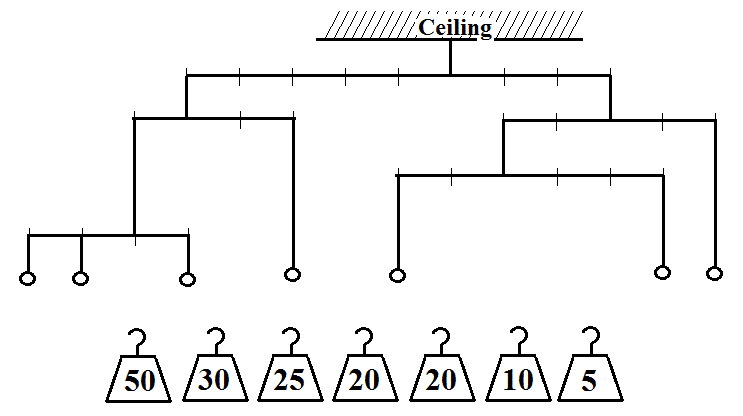
The April Puzzle: Can you arrange these seven weights from left-to-right to make this mobile perfectly balanced? Each weight is used only once.

Hall of Fame (April Puzzle Solvers):
Rocky S. Stone (NM)
Keith Gilbert (NM)
Harold Gaines (KS)
Terry Lauritsen (NM)
Mike Arms (NM)
Ross Goeres (NM)
Jerry W Barrington (OH)
Ian Tafoya (NM)
Ted Cloak (NM)

MARCH '10 PUZZLE - "Thar She Goes!"

Courtesy Saxon Math Stumpers.

Two uniform rods of equal length and unequal masses are connected by a massless and frictionless hinge. Initially, the rods are at rest, forming an equilateral triangle with a frictionless surface. At time t = 0 the lower ends of the rods begin to slide apart with only the force of gravity acting upon the system.

The March Puzzle: When the system comes to rest, how far has the hinge moved horizontally from its original position?

Hall of Fame (March Puzzle Solvers):
John Geohegan (NM)
John R. Lopez (NM)
Mike Arms* (NM)
Ross Goeres (NM)

FEBRUARY '10 PUZZLE - "Big Crowd at the Inn"

Courtesy seventeenth-century France.

41 persons eat at an inn. The total bill is 40 sous and each man pays 4 sous, each woman 3, and each child 1/3 sou.

The February Puzzle: How many men, women, and children were there?

Hall of Fame (February Puzzle Solvers):
Mike Arms (NM)
Rocky S. Stone (NM)
Harold Gaines (KS)
Keith Gilbert (NM)
Ross Goeres (NM)
Ian Tafoya (NM)
Eric Hanczyc (WA)
Margaret Mavretich (NM)
Ted Cloak (NM)
Bob Schmidt (NM)
Bob Carroll (NM)

JANUARY '10 PUZZLE - "Time?"

Adapted from Intriguing Mathematical Problems by Oswald Jacoby, with W. H. Benson.

Simpkins and Green made arrangements to meet at the railroad station to catch the 8:00 train to Philadelphia. Simpkins thinks that his watch is twenty-five minutes fast, although it is in fact ten minutes slow. Green thinks his watch is twenty minutes slow, while it has actually gained five minutes.

The January Puzzle: What will happen if both men, relying upon their watches, try to arrive at the station five minutes before train time?

Hall of Fame (January Puzzle Solvers):
Rocky S. Stone (NM)
Mike Arms (NM)
Eric Hanczyc (WA)
Keith Gilbert (NM)
Ken Hessel (NM)
Harold Gaines (KS)

DECEMBER '09 PUZZLE - "The Absent-Minded Rider"

Submitted by Dave Thomas

A bike enthusiast often rides several miles (mostly downhill) to his favorite lunch spot, Dan's Diner. He wanted to compare his average speed getting to the diner to his average speed for the more difficult return. The rider zeroed out his trusty Schwinn speedometer, and then used it to find that his average speed getting to lunch was 12 miles per hour (mph). After dining, however, the rider forgot to re-set the speedometer. Upon his return from lunch, the cyclist observed that the average cycling speed for the entire round trip was 9 mph. But, the rider still didn’t know what his return speed was.

The December Puzzle: What was the rider’s average speed on his return from lunch?

Hall of Fame (December Puzzle Solvers):
Bob Carroll (NY)
Rocky S. Stone (NM)
Paul Braterman (UK)
Eric Hanczyc (WA)
Keith Gilbert (NM)
Harold Gaines (KS)
Mike Arms (NM)
Ross Goeres (NM)
Ian Tafoya (NM)
Andrew Kennedy (MO)

NOVEMBER '09 PUZZLE - "What Comes Next?"

Submitted by Dave Thomas

The November Puzzle: What is the next number in the sequence 1, 7, 23, 63, 159, 383…?

Hall of Fame (November Puzzle Solvers):
Mike Arms (NM)
Rocky S. Stone (NM)
Harold Gaines (KS)
Ross Goeres (NM)
John Geohegan (NM)
Bob Carroll (NY)

OCTOBER '09 PUZZLE - "The Empty Flask"

Adapted from Intriguing Mathematical Problems by Oswald Jacoby, with W. H. Benson.

An apothecary found six flasks capable of holding 16, 18, 22, 23, 24, and 34 fluid ounces respectively. He filled some with distilled water, and then filled all but one of the rest with alcohol, noting that he had used precisely twice as much alcohol as water.

The October Puzzle: Which flask was left over? And which flasks were used for water, and which for alcohol?

Hall of Fame (October Puzzle Solvers):
Rocky S. Stone (NM)
Eric Hanczyc (WA)
Harold Gaines (KS)
Roy Thearle (UK)
Ross Goeres (NM)
Mike Arms (NM)

SEPTEMBER '09 PUZZLE - "The Six Knights"

Submitted by John Geohegan.

A small 3x4 chessboard has three black knights () and three white knights () as shown.

The September Puzzle: Show how to achieve the following position after 16 knight moves. (A knight moves two squares horizontally or vertically and one square vertically or horizontally, all combined as one move):

Hall of Fame (September Puzzle Solvers):
Ross Goeres (NM)
Rocky S. Stone (NM)

AUGUST '09 PUZZLE - "Fibonacci’s Metric Converter"

Submitted by Dave Thomas.

While on an expedition to Canada, an American scientist noticed a metric conversion factor hidden in the Fibonacci Series, which starts with two 1’s as the first two elements. Each subsequent element is the sum of the two preceding ones: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … . During numerous mental conversions between miles and kilometers, the scientist noticed that, if a given element of the series represented a distance in miles, the following element was close to the equivalent distance in kilometers. For example, 3 miles is close to 5 kilometers; 5 miles is close to 8 kilometers, and so on.

The August Puzzle: For which two consecutive elements of the Fibonacci series is their ratio closest to the actual number of kilometers in a mile? For which two consecutive elements is the estimation error, in meters, the smallest?

The August UBER-Puzzle: What are the two integers less than 20 which, if taken as the first two elements of the series, yield at least one conversion in the series with an estimation error of less than two meters?

What is "Estimation Error in Meters"? Consider 100 miles ~ 161 kilometers. The actual number of kilometers in 100.0 miles is 100*1.609344 = 160.934 km, which is .066km (66 meters, 65.6 m for the truly geeky) from the "goal" of 161.000 km.
For 100mile ~ 161km, then, the "Estimation Error" is about 66 meters.

Hall of Fame (August Puzzle Solvers):
Harold Gaines (KS)
John Geohegan (NM)
Ross Goeres (NM)
Mike Arms (NM)

JULY '09 PUZZLE - "Bargain Day"

Adapted from "Intriguing Mathematical Problems" by Oswald Jacoby and William Benson

On the final day of his close-out sale, a merchant hastily disposed of two lamps at the bargain price of $12 apiece. He estimated that he must have made some net profit on the combined transactions, since he made a 25 percent profit on one, and only took a 20 percent loss on the other.

The July Puzzle: Was he correct in his estimate?

Hall of Fame (July Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Ross Goeres (NM)
Bob Carroll (NY)
Rocky S. Stone (NM)
Harold Gaines (KS)
Eugene Aronson (NM)
Roy Thearle (UK)
Mike Arms (NM)

JUNE '09 PUZZLE - "The Big Shakedown"

Submitted by Dave Thomas

At a Seismology conference, several scientists attending Session A (Sustained Shaking Events) celebrated the meeting by having every attendee shake hands with everyone else in the room. In the next room, all the participants of parallel Session B (Shakytown After the Big One), similarly shook hands all around.

The June Puzzle: If the number of handshakes for Session B was exactly 50 more than for Session A, how many scientists were in Sessions A and B respectively?

Hall of Fame (June Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Mike Arms (NM)
Ross Goeres (NM)
Harold Gaines (KS)
Keith Gilbert (NM)
Bob Carroll (NY)
Eugene Aronson (NM)
Rocky S. Stone (NM)
Roy Thearle (UK)

MAY '09 PUZZLE - "Mystery on the Second Floor"

Submitted by Ross Goeres (adopted from The Economist, April 18, 2009)

There are three light switches on the ground-floor wall of a three-story house. Two of the switches do nothing, but one of them controls a bulb on the second floor. When you begin, the bulb is off. You can only make one visit to the second floor.

The May Puzzle: How do you work out which switch is the one that controls the light?

Hall of Fame (May Puzzle Solvers):
Rocky S. Stone (Tijeras, NM)
Keith Gilbert (NM)
Ken Hessel (NM)
Bob Carroll (NY)

APRIL '09 PUZZLE - "Monkey Madness"

Submitted by Eugene Aronson

On a desert island, five men and a monkey gather cocoanuts all day, and then sleep. One man awakens. He divides the cocoanuts into five equal shares. There is one left over, which he gives to the monkey. He hides his share and goes to sleep. The next man then awakens and does the same, and so on for all the men.

The April Puzzle: What is the minimum number of cocoanuts originally present?

Hall of Fame (April Puzzle Solvers):
Rocky S. Stone (Tijeras, NM)
K Sengupta (Calcutta,INDIA)
Harold Gaines (KS)
Eric Hanczyc (WA)
Ross Goeres (NM)
Mike Arms (NM)

 

MARCH '09 PUZZLE - "Back to the Ponderosa"

Submitted by Dave Thomas

Three brothers, Joe, Adam, and Hoss, can together pick twice as many goobers per hour as Joe alone, and three times as many as Adam alone.

The March Puzzle: if the slowest picker can pick a pound per hour, how fast can the brothers pick by themselves, and as a team?

Hall of Fame (March Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Mike Arms (NM)
Harold Gaines (KS)
Ross Goeres (NM)
Eric Hanczyc (WA)
Keith Gilbert (NM)
Eugene Aronson (NM)
Roger Hart-York (NM)
Ken Lynch (TX)

 

FEBRUARY '09 PUZZLE - "A MATHEMATICAL JOKE"

Submitted by John Geohegan

The following problem was published as problem E163 in the American Mathematical Monthly, 1935, and reprinted by Ross Honsberger in Mathematical Morsels, 1978, as "A Mathematical Joke" What's the answer, and what's the joke?

A man purchased at a post-office some one-cent stamps, three-fourths as many two's as one's, three-fourths as many five's as two's, and five eight-cent stamps. He paid for them all with a single bill, and there was no change.

The February Puzzle: How many stamps of each kind did he buy?

Hall of Fame (February Puzzle Solvers):
Rocky S. Stone (Tijeras, NM)
Ross Goeres (NM)
Harold Gaines (KS)
Eric Hanczyc (WA)
Mike Arms (NM)

 

JANUARY '09 PUZZLE - "WHAT COMES NEXT?"

Submitted by Dave Thomas

What is the next number in the sequence

3, 8, 14, 23, 37, 58?

Hall of Fame (January Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Rocky S. Stone (Tijeras, NM)
Bob Carroll (NY)
Eric Hanczyc (WA)
Kent Langsteiner (NM)
Cathy Burnell (NM)
Harold Gaines (KS)
Roy Thearle (UK)
Diane Marsh (TX)
Ross Goeres (NM)

 

DECEMBER '08 PUZZLE - "AGAINST THE ODDS"

Submitted by John Geohegan

Three cards are to be selected at random from a packet of playing cards.

The December Bonus: If the odds are 11 to 2 against all three being spades, how many cards are in the packet and how many are spades?

Hall of Fame (December Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Dave Thomas (NM)
Harold Gaines (KS)
Keith Gilbert (NM)
Eugene Aronson (NM)
Ken Lynch (TX)
Roy Thearle (UK)
Ross Goeres (NM)

 

NOVEMBER '08 PUZZLE - "ELECTORAL CLOUT"

Submitted by Dave Thomas

In the near future, many of the 50 states of the union, including New Mexico and Texas, will have different numbers of congressional representatives than at present. In the presidential electoral college, the number of electors per state equals that state’s number of congressmen, plus two (for the state’s senators). The number of congressmen is directly proportional to the state’s population. If the future number of congressmen in Texas is eight times that of New Mexico, then New Mexico would realize 20% more clout with the electoral college than with strict proportional representation, while Texas would realize 10% less clout.

The November Bonus: What is the future number of congressional representatives nationwide? In New Mexico? In Texas?

HINT: in this hypothetical Future, the number of congressmen is NOT federally mandated as 438.

Hall of Fame (November Puzzle Solvers):
John Geohegan (NM)

 

OCTOBER '08 PUZZLE - "MARKET MELTDOWN"

Submitted by Dave Thomas

Investor Henry “Hank” Swank uses the services of “Todo Toro” discount brokers, which charges $10.00 for each buy/sell transaction. On Monday, he used the service to buy 250 shares of FBNC (Fly By Night Corp.), at $60.00 per share. By Tuesday, these stocks had increased in value by 60%, and Hank decided to sell. By the time the sale transaction went through, however, the volatile stocks had lost 3/8 of their value.

The October Bonus: What was Hank’s Gain or Loss?

Hall of Fame (October Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Eric Hanczyc (WA)
Keith Gilbert (NM)
Ross Goeres (NM)
Eugene Aronson (NM)

 

SEPTEMBER '08 PUZZLE - "THE SOCIAL SECURITY NUMBER"

Submitted by John Geohegan

Reading a social security number consisting of the 9 digits, 1 through 9 though not in that order, from left to right, the first two digits form a number divisible by 2, the first three digits form a number divisible by three, the first four digits form a number divisible by four, and so on through all nine digits so that the entire nine-digit number is divisible by 9.

The September Bonus: What is the number?

Hall of Fame (September Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Dave Thomas (NM)
Eric Hanczyc (WA)
Ross Goeres (NM)
Eugene Aronson (NM)
Ken Lynch (TX)

 

AUGUST '08 PUZZLE - "The Time Is...?"

Submitted by Dave Thomas (adapted from Sam Loyd)

As a man was strolling through downtown, he popped into the office of the Ministry of Puzzles. He asked the receptionist "Good morning. Do you have the time?" The receptionist answered "Simply add one quarter of the time from midnight until now to half the time from now until midnight, and you will have the correct answer."

The August Bonus: What time was it?
Double Bonus: Had the man said “Good afternoon…” instead, what time would it have been?

Hall of Fame (August Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Keith Gilbert (NM)
John Geohegan (NM)
Ross Goeres (NM)
Harold Gaines (KS)
Eric Hanczyc (WA)
Bob Carroll (NY)
Eugene Aronson (NM)

 

JULY '08 PUZZLE - "THE CHICKEN OR THE EGG?"

Submitted by Dave Thomas

A New Mexican chicken farmer hired a consultant recently laid off from Los Alamos Lab. After much study, the consultant announced that "One and a half hens can lay one and a half eggs in one and a half days."

The July Bonus: How many hens are needed for the farmer to produce a dozen eggs in six days?

Hall of Fame (July Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Keith Gilbert (NM)
Eric Hanczyc (WA)
Ross Goeres (NM)
Eugene Aronson (NM)
Ken Lynch (TX)
Harold Gaines (KS)

 

JUNE '08 PUZZLE - "TWO TRAINS"

Submitted by John Geohegan

(appeared as problem E1386 in the American Mathematical Monthly, 1959, and is reprinted in Mathematical Morsels, by Ross Honsberger, 1978.)

In overtaking a freight, a passenger train which is x times as fast takes x times as long to pass it as it takes the two trains to pass when going in opposite directions.

The June Bonus: Find x

Hall of Fame (June Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Eric Hanczyc (WA)
Eugene Aronson (NM)
Keith Gilbert (NM)
Roger Kilgore (NM)
Ross Goeres (NM)

 

MAY '08 PUZZLE - "Daylight Savings Downside"

Submitted by Dave Thomas

A commuter’s van pool drops him off behind the police station every night at 6 PM, and his wife arrives there at exactly 6 PM to pick him up. On the first day of Daylight Savings Time, however, the man had remembered to turn his clock an hour ahead, but his wife had forgotten completely. Finding himself without a ride (because of his wife’s thinking that it was 5 PM), the commuter started walking home. His wife came across him walking down the road some time later, and picked him up for the ride back home. The commuter’s wife ended up getting back home eight minutes earlier than she had expected.

The May Bonus: How long was the man’s walk before his wife picked him up?

Hall of Fame (May Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Ross Goeres (NM)
Eugene Aronson (NM)
Eric Hanczyc (WA)
Ken Lynch (TX)

 

APRIL '08 PUZZLE - "JACKS OF THREE TRADES"

Submitted by Dave Thomas

The MegaGenomics Corporation placed a want ad for a position requiring knowledge of biology, mathematics and computer science. Of the 60 respondents who submitted applications, 46 had training in biology, 40 had training in mathematics, 43 had training in computer science, and 10 had no training in either biology, mathematics or computer science. There are three times as many applicants with mathematics-only backgrounds as with computer-science-only backgrounds; and, there are twice as many applicants with biology-only backgrounds as with computer-science-only backgrounds.

The April Bonus: How many of the applicants had undergone training in all three fields?

Hall of Fame (April Puzzle Solvers):
Steve's Brother in Law (CA)
K Sengupta (Calcutta,INDIA)
Keith Gilbert (NM)
Eric Hanczyc (WA)
Eugene Aronson (NM)
Ross Goeres (NM)

 

MARCH '08 PUZZLE - "CORDIALITY BEFORE CORDIALS"

Submitted by Ken Lynch

A party of three couples (Ben and Alice being one couple) enters a room and shakes hands based on these conditions: a) Once you shake a person's hand, you do not shake with that person again. b) Couples do not shake hands with each other. Alice asked each person how many hands he/she shook, and everyone gave her a different answer.

The March Bonus: How many hands did Ben shake?

Hall of Fame (March Puzzle Solvers):
Steve's Brother in Law (CA)
K Sengupta (Calcutta,INDIA)
Eugene Aronson (NM)
Ross Goeres (NM)
Eric Hanczyc (WA)

 

FEBRUARY '08 PUZZLE - "Playing with Fire"

Submitted by Paul Braterman

Can you arrange five matches so that each of them touches three and only three others? The matches may touch at any point, but you are not allowed to bend or break them.

Hall of Fame (February Puzzle Solvers):
Steve's Brother in Law (CA)
K Sengupta (Calcutta,INDIA)
Eugene Aronson (NM)
Eric Hanczyc (WA)
Ross Goeres (NM)
Bob Schmidt (NM)

 

JANUARY '08 PUZZLE - "The Flower and the Lake"

Submitted by Dave Thomas, after Longfellow

A long-stemmed flower extends straight up from the bottom of a lake, extending 8 inches above the lake’s surface. A man in a rowboat observes that, when he pulls on the flower, it touches the lake’s surface at a distance of 20 inches from the stem’s original position.

The January Bonus: how deep is the lake?

Hall of Fame (January Puzzle Solvers):
Rocky S. Stone (Tijeras, NM)
Steve's Brother in Law (CA)
K Sengupta (Calcutta,INDIA)
Keith Gilbert (NM)
Ross Goeres (NM)
John Lopez (NM)
Paul Braterman (NM)
TSgt Michael K Stage(NM)

 

DECEMBER '07 PUZZLE - "The Crazy Clocks"

Submitted by Dave Thomas

Based on a True Story!

On the long drive home from a field trip to fabled Shark Tooth Ridge, a paleontologist passenger observes a discrepancy between the car’s digital clock and his cell phone’s digital clock. Both clocks show hours and minutes only. Sometimes the cell phone reads two minutes ahead of the car’s clock, and sometimes it reads just one minute ahead.

The December Bonus:If the clocks appear to be two minutes apart for twice as long as they appear to be one minute apart, and assuming both clocks can keep perfect time, what is the actual time difference (in seconds) between the clocks?

Hall of Fame (December Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Steve's Brother in Law(CA)
Eugene Aronson (NM)
Ross Goeres (NM)
Nick Seigal (Eugene OR)

 

NOVEMBER '07 PUZZLE - "By The Numbers"

Submitted by Ken Lynch (from Douglas Hofstadter’s Metamagical Themas)

Complete the following sentence: In this sentence, the number of occurrences of 0 is _, of 1 is _, of 2 is _, of 3 is _, of 4 is _, of 5 is _, of 6 is _, of 7 is _, of 8 is _, and of 9 is _. Each blank is to be filled with a numeral of one or more digits, written in decimal notation.

The November Bonus: Find two solutions.

Hall of Fame (November Puzzle Solvers):
K Sengupta (Calcutta,INDIA)
Steve's Brother in Law(CA)
Eugene Aronson (NM)
Ross Goeres (NM)
Charles Vaughn (Rotterdam, NL)

 

OCTOBER '07 PUZZLE - “Super Bounce”

Submitted by Dave Thomas

A large ball and a very small ball are dropped from a height of five feet, as shown. Both balls are perfectly elastic ("bouncy"). When the large ball bounces, it then impacts the small ball, bouncing it upward as shown.

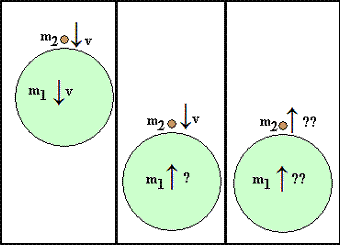
The October Bonus: What is the highest that the small ball can bounce?

(A) 5 feet
(B) 10 feet,
(C) 15 feet,
(D) 20 feet,
(E) 45 feet.

Hall of Fame (October Puzzle Solvers):
K Sengupta (Calcutta, INDIA)
Keith Gilbert (NM)
Eugene Aronson (NM)

 

SEPTEMBER '07 PUZZLE - “Trisecting a Clock Face”

Submitted by Gene Aronson

At what time(s) do the hour, minute, and second hands of a 12-hour clock divide the face into three equal segments, either precisely or as close as possible? Assume a perfectly smooth motion, and answer to within one second.

Hall of Fame (September Puzzle Solvers):
K Sengupta (Calcutta, INDIA)
Ross Goeres (NM)
John Lopez (NM)

 

AUGUST '07 PUZZLE - “Gearing Up for a Mystery!”

Submitted by John Geohegan

Here's a puzzle from chapter 9, "Patterns and Primes", of Martin Gardner's Sixth Book of Mathematical Games from Scientific American:

Shown below are two meshing gears marked with arrows pointing toward each other. The larger gear has 181 teeth.

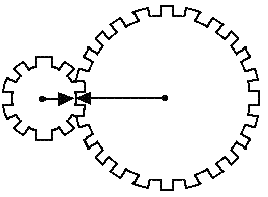
The August Bonus:

How many turns must the smaller gear make before the arrows again point to each other?

Hall of Fame (August Puzzle Solvers):
Steve's brother-in-law (CA)
K Sengupta (Calcutta, INDIA)
Ross Goeres (NM)
Eugene Aronson (NM)

 

JULY '07 PUZZLE - “The Poorly-Planned Polygraph”

Submitted by Dave Thomas

Paranormal investigator George Bradford had worked for months setting up an elaborate blind test of polygraphs. And here he was at last, taking data from four individuals who had all promised to abide by the strict experimental protocols. The first part of the experiment had all four subjects meet in private, where they witnessed one of their number hide a toy bunny. Then, each subject was told to make two statements to polygraph testers (and other observers) about the "incident": one true, and one false. Only later, as the correct answers were revealed, could the researchers see if the polygraph machines used alongside were giving correct answers or not.

As the four subjects gave their two statements each, George turned white, as he realized that simple logic would allow the polygraph examiners to decide which statements were True or False, making it very easy for them to cheat.

Here are the four pairs of statements:

Arnie said: It wasn't me. It was Carl.

Betty said: It was Arnie. It wasn't Carl.

Carl said: It wasn't Betty. It wasn't Debbie.

Debbie said: It wasn't Carl. It was me!

The July Bonus:

(A) Which are lies, and which are true?

(B) Who hid the bunny?

Hall of Fame (July Puzzle Solvers):
K Sengupta (Calcutta, INDIA)
Steve's brother-in-law (CA)
Ross Goeres (NM)
Roy Thearle (UK)
Eric Hanczyc (WA)
Eugene Aronson (NM)

 

JUNE '07 PUZZLE - “Number Cipher!”

Submitted by Ken Lynch

Consider the following sum:

2831 + 101461 + 513122 = 617414

The June Bonus:

(A) Replace each digit with a different digit to make another correct addition problem; no digit may replace itself. It’s a Numerical Cipher!

(B) Can you replace each digit with a letter to spell the names of four of the United States?

Hall of Fame (June Puzzle Solvers):
K Sengupta (Calcutta, INDIA)
Ray Comas (OH)
Ross Goeres (NM)
Eugene Aronson (NM)
Eric Hanczyc (WA)

 

May '07 PUZZLE - “What is the Product?”

Submitted by John Geohegan

The following puzzle is from "The Surprise Attack in Mathematical Problems", by L.A.Graham. Only the words have been changed.

Three digits, a,b,and c have been used to form the three digit numbers abc, bca, and cab, which have then been multiplied to make a 9-digit product. The number 234,235,286 is not the product, but 6 is in the proper place and the other digits are disordered.

The May Bonus: What is the Product?

Hall of Fame (May Puzzle Solvers):
K Sengupta (Calcutta, INDIA)
Ray Comas (OH)
Ross Goeres (NM)
Eugene Aronson (NM)
Eric Hanczyc (WA)
Paul Flocken (NC)

 

April '07 PUZZLE - “Derek's Appointment”

Derek bicycles from Abercrombie to Fitch for a one o'clock appointment. After pedalling at a steady rate for 42 kilometers, he increases his speed by 3 km/hr and arrives at precisely 1:00. If he hadn't increased his speed he would have been 18 minutes late, and if he had made the whole trip at the greater speed he would have arrived, exhausted, 42 minutes early.

The April Bonus: What time did Derek leave Abercrombie?

Hall of Fame (April Puzzle Solvers):
Dave Thomas (NM)
Keith Gilbert (NM)
Ray Comas (OH)
Bob Schmidt (NM)
Ross Goeres (NM)
Eugene Aronson (NM)

 

March '07 PUZZLE - “Alice and Bob and the Tossed Coins”

submitted by Ray Comas (Ohio)

Alice and Bob each have a collection of coins. Alice has one more coin than Bob. Alice tosses all of her coins in the air, and counts how many come up heads. Then Bob does the same with his coins.

The March Bonus: Assuming all coins are fair coins, what is the probability that Alice will produce more heads with her coin toss than Bob does with his coin toss?

Hall of Fame (March Puzzle Solvers):
K Sengupta (Calcutta, INDIA)
Roy Thearle (UK)
Bob Carroll (NY)
Eric Hanczyc (WA)
Paul Braterman (NM)
Keith Gilbert (NM)
Eugene Aronson (NM)
Ross Goeres (NM)

 

February '07 PUZZLE - “SORTING SUNDRY SIBLINGS”

submitted by Dave Thomas

In the family of Steve and Sally Starling, each boy has twice as many brothers as sisters, while each girl has three times as many brothers as sisters.

The February Bonus: How many Starling Siblings are there?.

Hall of Fame (February Puzzle Solvers):
K Sengupta (Calcutta, INDIA)
Ray Comas (OH)
Harry Murphy (NM)
Harold Gaines (KS)
Roy Thearle (UK)
John Geohegan (NM)
Christian Winteler, (Switzerland)
Eric Hanczyc (WA)
Bob Carroll (NY)
Eugene Aronson (NM)
Ross Goeres (NM)
Bob Schmidt (NM)

 

January '07 PUZZLE - “BETTING ON CHUCK-A-LUCK”

submitted by John Geohegan

In the carnival game called Chuck-a-Luck, the player bets on a number, one through six. Three dice are then rolled and if the player's number comes up once, he receives his original bet, for instance a dollar, plus another dollar. If his number comes up two or three times, he receives his original bet plus another two or three dollars. The smooth-talking game operator suggests that since the chance of the chosen number showing up on any die is one out of six, the player has a fifty-fifty chance of getting his number at least once on the three dice, and the payoffs of two or three dollars make the odds to the player's advantage.

But really, how much does the player stand to win or lose on an average bet of one dollar?

Hall of Fame (January Puzzle Solvers):
K Sengupta (Calcutta, INDIA)
Dave Thomas (NM)
Keith Gilbert (NM)
Ray Comas (OH)
Eugene Aronson (NM)
Grey Wolf (anonymous lurker on the Internet)
W. Kevin Vicklund (MI)

 

DECEMBER '06 PUZZLE - "Grazing Grass by the Numbers!"

submitted by K Sengupta (Calcutta, INDIA)

A grassland can support 63 sheep for 5 days; or, 22 cows for 9 days; or, 16 cows and 5 sheep indefinitely. The grass grows at a constant rate per unit time in the grassland.

Three friends Pedro, Quentin and Rhett jointly hire the grassland for $6930. They agree that the share of rent paid by any given friend would be determined in accordance with the total amount of grass consumed by his pets.

Pedro grazes 9 cows and 16 sheep for a period of 20 days; Quentin grazes 10 cows and 3 sheep for 28 days and, Rhett grazes 6 cows and 13 sheep for 27 days.

The December Bonus: Determine the respective share of rent payable by Pedro, Quentin and Rhett on the grassland from the information inclusive of the foregoing statements.

Hall of Fame (December Puzzle Solvers):
John Geohegan (NM)
Ray Comas (OH)
Eugene Aronson (NM)

 

NOVEMBER '06 PUZZLE - "Squaring,Cubing,Ten Digits -Oh My!"

submitted by John Geohegan

The square and the cube of a certain whole number can be written using each of the ten digits, 0 through 9, exactly once.

The November Bonus: What is that certain number?

Hall of Fame (November Puzzle Solvers):
K Sengupta (Calcutta, INDIA)
Harold Gaines (KS)
Ray Comas (OH)
Eric Hanczyc (WA)
Eugene Aronson (NM)
Bob Schmidt (NM)

 

OCTOBER '06 PUZZLE - "Starting the Election Party"

submitted by Dave Thomas

It is Election Night, and candidate Bill E. Bob is pacing around election headquarters. With 60% of precincts reporting, Bob is leading with 60% of the vote.

The October Bonus:

(a) If only half of the remaining voters (40% of precincts) vote for Bob, will he win?

(b) At what percentage of precincts reporting will Bill E. Bob be justified in popping the cork off of a champagne bottle?

Hall of Fame (October Puzzle Solvers):
W. Kevin Vicklund (MI)
Grey Wolf (anonymous lurker on the Internet)
K Sengupta (Calcutta, INDIA)
Eric Hanczyc (WA)

 

SEPTEMBER '06 PUZZLE - "FAIR TOSSES"

submitted by Ken Lynch

Alice and Bob toss a fair coin alternately to play a game where the first to toss "heads" immediately after the other tosses a "tail" wins. Alice tosses first.

The September Bonus: What is the probability that:

a) Alice wins on her 1st toss

b) Bob wins on his 1st toss

c) Alice wins on her 3rd toss

d) Bob wins on his 5th toss

e) Alice wins.

Hall of Fame (September Puzzle Solvers):
K Sengupta (Calcutta, INDIA)
Eric Hanczyc (WA)
W. Kevin Vicklund (MI)
Harold Gaines (KS)
Eugene Aronson (NM)

 

AUGUST '06 PUZZLE - "THE PIRATE CHEST"

submitted by Dave Thomas

You have been captured by Pirates while sailing the Carribean, and have been brought before their gruff Captain. With a sinister snarl, he barks "I've a chest here that holds 120 pounds of pure gold coins. Some of these coins be decloons [10 ounces each], and the rest be triploons [three ounces each]. Now, mate, if ye can tell me exactly how many decloons and triploons are in my chest, ye walks away a free man. Get it wrong, and ye'll be walkin' the Plank!" After another pirate suggested that the riddle was perhaps overly challenging, the Captain snorted, and then offered a hint: "Awright, matey - the number of decloons times the number of triploons couldn't be larger!"

The August Bonus: For your life - how many decloons and how many triploons are in the chest?

Hall of Fame (August Puzzle Solvers/HONORARY PIRATES):
Jesse Johnson (NM)
K Sengupta (Calcutta, INDIA)
Bob Carroll (NY)
Harold Gaines (KS)
Jim Mitchell (NM)
Eric Hanczyc (WA)
Ross Goeres (NM)
Ken Lynch (TX)
Ray Comas (OH)
Eugene Aronson (NM)
Grey Wolf (anonymous lurker on the Internet)
Marek Ctrnact (Czech Republic)
Jeff Elliott (Spanish colony of California)
Christian Winteler (Switzerland)
John M. Sovitsky (VA)
Roy Thearle (UK)
W. Kevin Vicklund (MI)
Calum mac Leoid (Pentamere)

 

JULY '06 PUZZLE - "THE LAW OF AVERAGES "

submitted by Dave Thomas & Ross Goeres

In a race along a two-kilometer-long track, you are required to travel the first kilometer at an average speed of 20 km/hour.

The July Bonus: (A) How fast must you travel on the second kilometer of track to achieve an overall average speed of 30 km/hour? (What's your off-the-hip estimate? And your Final Answer?) (B) How fast must you travel on the second kilometer of track to achieve an overall average speed of 40 km/hour? (C) What have you learned, Grasshopper, about trying to average ratios?

Hall of Fame (July Puzzle Solvers):
Bob Carroll (NY)
Jen Niver (NM)
Eric Hanczyc (WA)
Eugene Aronson (NM)
Harold Gaines (KS)
Keith Gilbert (NM)
K Sengupta (Calcutta, INDIA)

 

JUNE '06 PUZZLE - "TOUCHED BY A TEN-FOOT POLE "

submitted by Gene Aronson

(Gene Aronson has submitted the following problem in slightly different form )

Mathematicians have shown that the following problem is workable, even though it looks like more information might be necessary. Knowing that it's workable makes it much easier to find the numerical answer.

A ten-foot pole floats in a large swimming pool shaped approximately as shown in the sketch below. As the pole makes one circuit around the pool (BLACK boundary), both ends of the pole bump continuously against the wall. During this circuit, point P on the pole, six feet from one end, traces out the smaller area labelled A (RED boundary).

.

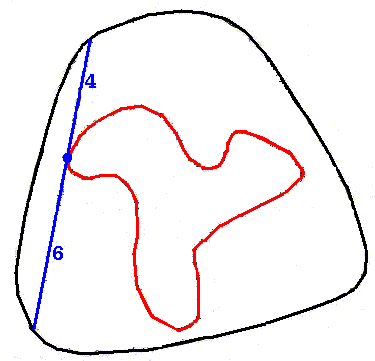
HOW MUCH SMALLER than the pool, in square feet, is area A?

Hall of Fame (June Puzzle Solvers):
Harold Gaines (KS)
K Sengupta (Calcutta, INDIA)
Gene Delloro (Toronto, ON)
Eric Hanczyc (WA)
Bob Carroll (NY)

 

MAY '06 PUZZLE - "Mr. Auber and Mr. Benatar "

submitted by K Sengupta of Calcutta, INDIA

The Identification (ID) Numbers allotted to Mr. Auber and Mr. Benatar are such that the numerical magnitude of the ID number allotted to Mr. Benatar is greater by 10 than the numerical magnitude of the ID number allotted to Mr. Auber. None of the two ID numbers contained any leading zeroes.

A mutual acquaintance, Mr. Cavalli , who is aware of the above facts ( but doesn't know the actual ID numbers of the two gentlemen), queried Mr. Auber and Mr. Benatar in turn about the sum of the digits in their ID Numbers. The responses elicited by him were respectively 44 and 27.

At this point, Mr. Cavalli requested Mr. Auber and Mr. Benatar give some additional information. Both gentlemen answered with a new question: "What are the smallest possible values for the two ID numbers?"

Thereafter, Mr. Cavalli was able to ascertain precisely the ID numbers of Mr. Auber and Mr. Benatar.

Then, The ID # of Mr. Auber = ? and, The ID # of Mr.Benatar = ?

Hall of Fame (May Puzzle Solvers):
Aaron Sullivan (AZ)
Harold Gaines (KS)
Eric Hanczyc (WA)
Bob Schmidt (NM)

 

APRIL '06 PUZZLE - "CIPHER ADDITION..."

submitted by John Geohegan

Here's an addition cryptarithm sent in by Ken Lynch. Difficult as it is to solve, composing it seems close to a miracle.

A P P R E C I A T I V E + I N C A P A C I T A T E + I N D E P E N D E N C E = P A R T I C I P A T E D

Hall of Fame (April Puzzle Solvers):
Ross Goeres (NM)
Harold Gaines (KS)
Eric Hanczyc (WA)
Eugene Aronson (NM)
Mike Denny (AZ)
Bob Schmidt (NM)

 

MARCH '06 PUZZLE - "The Race of the Weights..."

submitted by John Geohegan

Weight-driven grandfather clocks use two weights. One drives the pendulum and causes the hands to turn, the other supplies power when the clock strikes either the hour or the half-hour. Problem #20 in L. A. Graham's "Ingenious Mathematical Problems and Methods" reads, "A weight-driven clock, striking the hour, and a single stroke for the half hour, is wound at 10:15 P.M. by pulling up both weights until they are exactly even at the top. Twelve hours later, the weights are again exactly even, but lowered 720 mm. What is the greatest distance they separated during the interval?"

Hall of Fame (March Puzzle Solvers):
Dave Thomas (NM)
Ross Goeres (NM)
Harold Gaines (KS)
Eugene Aronson (NM)
Eric Hanczyc (WA)
Mike Denny (AZ)

 

FEBRUARY '06 PUZZLE - "My Candle Burns at One End..."

submitted by John Geohegan

Two “identical” candles are lighted at the same time. One will burn out in five hours, the other in eight hours. How long will it be before one is 2.2 times the length of the other, if (a) “identical” means the candles burn at the same rate, and start out having different lengths, AND (b) “identical” means the candles start out having the same lengths, and burn at different rates?

Hall of Fame (February Puzzle Solvers):
William Decorie (IL) (b)
Ross Goeres (NM) (a,b)
Keith Gilbert (NM) (a,b)
Harold Gaines (KS) (a,b)

 

JANUARY '06 PUZZLE - "SCALING UP"

submitted by Dave Thomas

A brilliant but warped scientist is persuaded to help a Hollywood mogul make a "King Kong" sequel, not by creating a giant ape, but by developing miniature humans, just one-hundredth their normal height. Designers have crafted a one-hundredth-scale set for the tiny humans to interact with a normal, life-sized gorilla.

The January Bonus (Warning - SPOILER!!) In Kong's fall from the scaled-down Empire State building, how many times faster than normal should the film be shot to give Kong a proper-looking plummeting rate?

Hall of Fame (January Puzzle Solvers):
William Decorie (IL)
John Geohegan (NM)
Harold Gaines (KS)

 

DECEMBER '05 PUZZLE - "CAPACITY"

submitted by Dave Thomas

Paul lives in Española, where the price of gasoline is $2.50 per gallon. There is a gas station near Albuquerque, 75 miles from Paul's house, which sells gas at $2.00 per gallon; his truck gets 30 miles per gallon. Paul schemes to save money by buying gas at the cheaper station in Albuquerque, and then cruising around his Española home.

The December Bonus: What is the minimum number of gallons that Paul's gas tank(s) would have to hold in order for his scheme to be feasible?

Hall of Fame (December Puzzle Solvers):
William Decorie (IL)
Bob Schmidt (NM)
John Geohegan (NM)
Ken Lynch (TX)

 

NOVEMBER '05 PUZZLE - What's Left Behind?

submitted by John Geohegan

A hole six inches long is drilled straight through the center of a solid sphere.

The November Bonus: What is the volume of the remaining material?

Hall of Fame (November Puzzle Solvers):

William Decorie (IL)
Bob Schmidt (NM)
Keith Gilbert (NM)
Click HERE for the Answer

 

OCTOBER '05 PUZZLE - Double Sixes

submitted by John Geohegan

In 1654, Chevalier de Méré approached Blaise Pascal with a question about a gambling game that had been played for hundreds of years. The house would bet even money that a player would roll at least one double-six in 24 rolls of a pair of dice.

The October Bonus: Did the house stand to make money on this bet?

Hall of Fame (October Puzzle Solvers):
William Decorie (IL)
Bob Schmidt (NM)
Ross Goeres (NM)
Ken Lynch (TX)

 

SEPTEMBER '05 PUZZLE - The Mirror of Time

submitted by John Geohegan

Mike's age is multiplied by seven if its digits are reversed, and one more digit is inserted. How old is Mike?

The September Bonus: How old is Mike?

Hall of Fame (September Puzzle Solvers):
William Decorie (IL)
Barry Spletzer (NM)
TexasSkeptic  (TX)
Bob Schmidt (NM)
Charles E. Oelsner (NM)
Kevin Webster (NM Lobo in WA)
Ken Lynch (TX)

 

AUGUST '05 PUZZLE - The Bargain Sale

Courtesy Sam Loyd

In describing his experiences at a bargain sale, Smith says that half his money was gone in just thirty minutes, so that he was left with as many pennies as he had dollars before, and but half as many dollars as before he had pennies.

The August Bonus: Now, how much did Smith spend?

Hall of Fame (August Puzzle Solvers):
John Geohegan (NM)
William Decorie (IL)
Eric Hanczyc (WA)
Charles E. Oelsner (NM)
Keith Gilbert (NM)
Bob Schmidt (NM)
TexasSkeptic  (TX)

 

JULY '05 PUZZLE - SELF-DIVISIBLE NUMBERS

Submitted by John Geohegan

New Scientist magazine publishes a new Enigma(math puzzle) each week. In the June 4 issue, the puzzle is to find the largest integer whose digits are all different (and do not include 0) that is divisible by each of its individual digits. Thus the number 248 is divisible by 2, 4, and 8 but so is 824 which is larger. The largest such integer is MUCH less than 987,654,321. Next month the solution will show how to cut this problem down to a reasonable size.

The July Bonus: What is the largest such integer?

Hall of Fame (July Puzzle Solvers):
William Decorie (IL)
TexasSkeptic  (TX)
Charles E. Oelsner (NM)
Ken Lynch (TX)

 

JUNE '05 PUZZLE - THE NO-COMMISSION BROKER

Submitted by Dave Thomas

There was once a broker of Yeti fur, highly prized for its luxuriant texture. This broker boasted that he took no commissions when either buying or selling the fur. The townsfolk wondered how he could possibly stay in business, but he was apparently quite prosperous. After years had passed, they finally found out the broker's secret -- he was caught using a biased scale. The rigged scale was arranged to be an ounce per pound short when buying, and an ounce per pound heavy when selling. The broker's final transaction involved an amount of Yeti fur that would have given him $30.00 of illicit profit.

The June Bonus: How much did the broker spend when buying the fur for his last transaction?

Hall of Fame (June Puzzle Solvers):
M. K. Johnson (NM)
John Geohegan (NM)
Harold Gaines (KS)
TexasSkeptic  (TX)
Pierre Scalise (AL)
Keith Gilbert (NM)
Ken Lynch (TX)

 

MAY '05 PUZZLE - THE MICRO-BREWMASTER

Submitted by TexasSkeptic

The Brownbagg Brewery's signature beer, Bob Brownbagg Barleywine, uses three strains of hops (Bitterbit, Flowergirl and Aromaroma) and three types of barley malt (Pale, Toasted and Burnt). The hops contribute Bitter, Aromatic, and Floral flavor fractions to the "wort" (unfermented beer syrup); the grains contribute color, complex carbohydrates ("unfermentable sugars") and glucose/maltose ("fermentable sugars"). Fermentation converts all the glucose/maltose into alcohol, one kg producing 500 ml of alcohol. The other components are not affected.

Grain yields

One kilogram of this grain	Pale Barley	Toasted Barley	Burnt Barley
produces this much fermentable sugar (g)	600	100	0
this much complex carbohydrate (g)	100	500	0
and this many units of color	0	100	600

Hops yields

One gram of this strain	Bitterbit	Flowergirl	Aromaroma
produces this much Bitter fraction (mg)	50	10	20
this much Aromatic fraction (mg)	20	30	60
and this much Floral fraction (mg)	30	70	30

The final product contains (per liter):

103.7 ml alcohol

51 g complex carbos

18.4 units color

72 milligrams Bitter fraction

86 mg Aromatic fraction

96 mg Floral fraction

And the Balance, water

The May Bonus: How much of each grain type and hop strain must the brewmaster purchase for one 6500 liter batch of Bob Brownbagg Barleywine?

Hall of Fame (May Puzzle Solvers):
Dave Thomas (NM)
Ken Lynch (TX)
Ross Goeres (NM)
John Geohegan (NM)
William J.Keith (PA)

 

APRIL '05 PUZZLE - JUGS

Submitted by Dave Thomas

World-renowned chemist Dr. Dweeb owned a 12-gallon jug full of sulfuric acid, and another smaller jug. He liked to make up his favorite 25% strength solution (with a quarter of the solution being H₂SO₄, and the rest good old H₂O) with a curious procedure: first, he poured acid from the 12-gallon jug to fill the smaller jug, and then he topped off the big jug with water. After the acid and water had been thoroughly mixed in the big jug, he drew off another small jugful, and again topped off the large jug with more water, arriving at his 25% solution.

The April Bonus: What's the capacity of the smaller jug?

Hall of Fame (April Puzzle Solvers):
Keith Gilbert (NM)
John Geohegan  (NM)
Bob Wood  (NM)
TexasSkeptic  (TX)
Harold Gaines (KS)
Ken Lynch (TX)

 

MARCH '05 PUZZLE - RACE AGAINST TIME

Submitted by Dave Thomas

This month's puzzle might just be harder than it may at first appear! It seems that two brothers from the famous puzzle-solving Answer family, Bobby and Al Answer, were trying out some new hot rod cars on the family's private race-track. Once both racers were up to their respective speeds (Bobby's car was going 120 miles per hour, and Al's was going 95 mph), they crossed the starting mark of the two-mile track just as the gun went off, and then maintained their respective speeds for 24 laps each.

The March Bonus: How much time passes until Bobby first catches up to Al?

At what position on the two-mile track (relative to the starting mark) does this occur?

Hall of Fame (March Puzzle Solvers):
Jesse Johnson (NM)
TexasSkeptic (TX)
Keith Gilbert (NM)
Ken Lynch (TX)
John Fleck (NM)

 

FEBRUARY '05 PUZZLE - THE BIG BEER BASH

Submitted by Dave Thomas

This month's puzzle is for today's mathematically-minded college frat rats and party-goers. The Kappa Kuppa K'rona fraternity was planning for the Big Bash. Usually, 10 cases of Spud Beer, which is 6 and 1/4 % alcohol by volume, are required for the Bash. (There are four 6-packs per case, and 12 ounces per beer, of course!). This year, however, crafty funds manager George Waldo Busch calculated that they wouldn't need to buy as many cases if they got "Beastie Beer" instead, since that brand has a mind-numbing 15 and 5/8% alcohol by volume.

The February Puzzle: How many cases of "Beastie Beer" should Busch Buy for the Big Bash?

Hall of Fame (February Puzzle Solvers):
John Geohegan (NM)
Marilyn Goodrich (NM)
TexasSkeptic (TX)
Harold H. Gaines (KS)
Mike Arms (NM)
Ken Lynch (TX)

 

JANUARY '05 PUZZLE - SOLVE FOR X

Submitted by John Geohegan

Fill in the x's with digits.

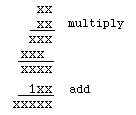
Hall of Fame (January Puzzle Solvers):
Marilyn Goodrich (NM)
Rod Earwood (NM)
Mark Maravetz (NM)
Ken Lynch (TX)

This is the Old Puzzle Archive. See NEW Puzzles!

NMSR SiteMap